Introduction to Exploratory and Confirmatory Factor Analysis (Using R)
Princeton University
4/11/23
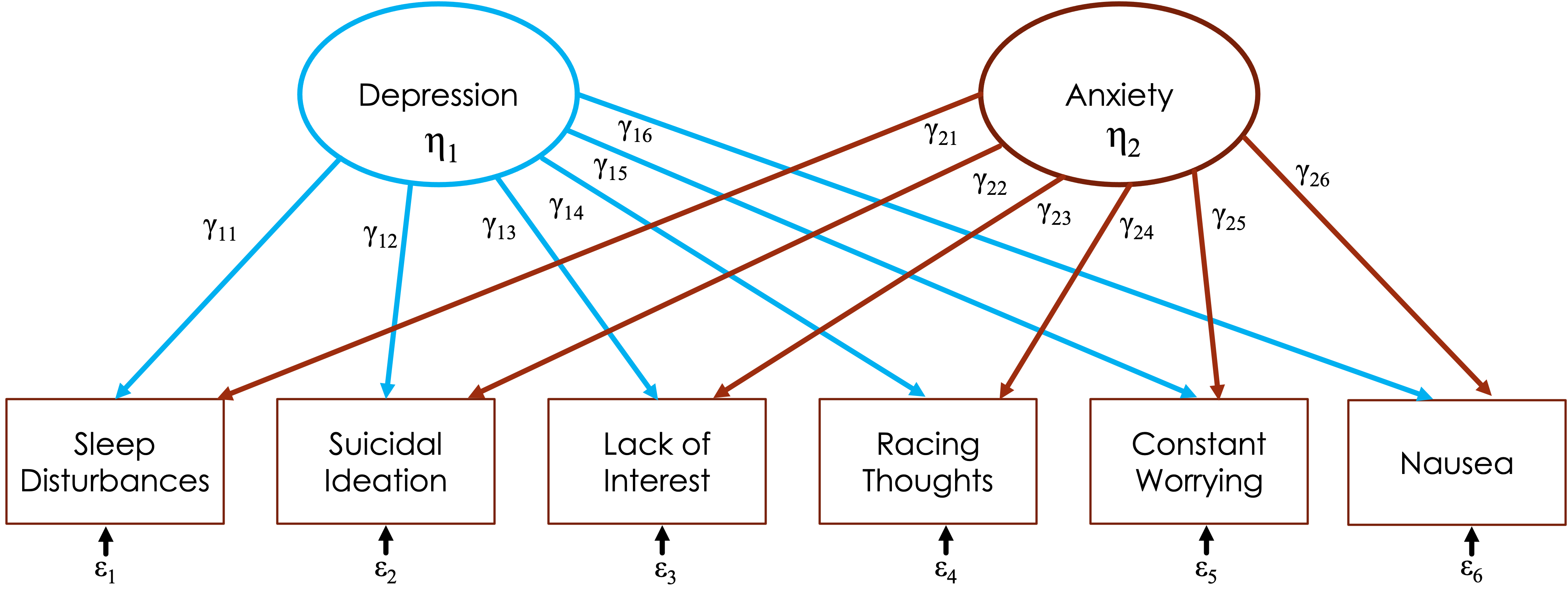
How does it work?
Let’s say we have 6 items in a scale:
Sleep disturbances (insomnia/hypersomnia)
Suicidal ideation
Lack of interest in normally engaging activities
Racing thoughts
Constant worrying
Nausea
FA “looks” at the relationships between these items and finds that some of them seem to hang together
How does it work?
Let’s say we have 6 items in a scale:
Sleep disturbances (insomnia/hypersomnia)
Suicidal ideation
Lack of interest in normally engaging activities
Racing thoughts
Constant worrying
Nausea
Some of these could cross-load
FA considers this and items load on all factors
Uses
Simplify data
- 6 variables to 2 variables
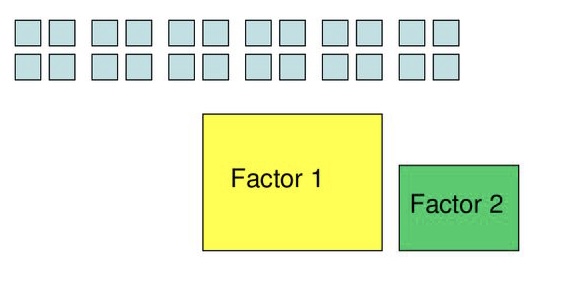
Uses
Identify underlying constructs
- Depression and anxiety
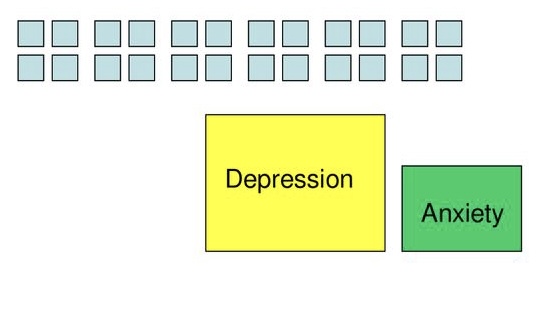
Partitioning Variance
- Variance common to other variables
- Communality \(h^2\): proportion of each variable’s/item’s variance that can be explained by the factors
- How much an item is related to other items in the analysis
- Communality \(h^2\): proportion of each variable’s/item’s variance that can be explained by the factors
- Variance specific to that variable
- Random measurement error
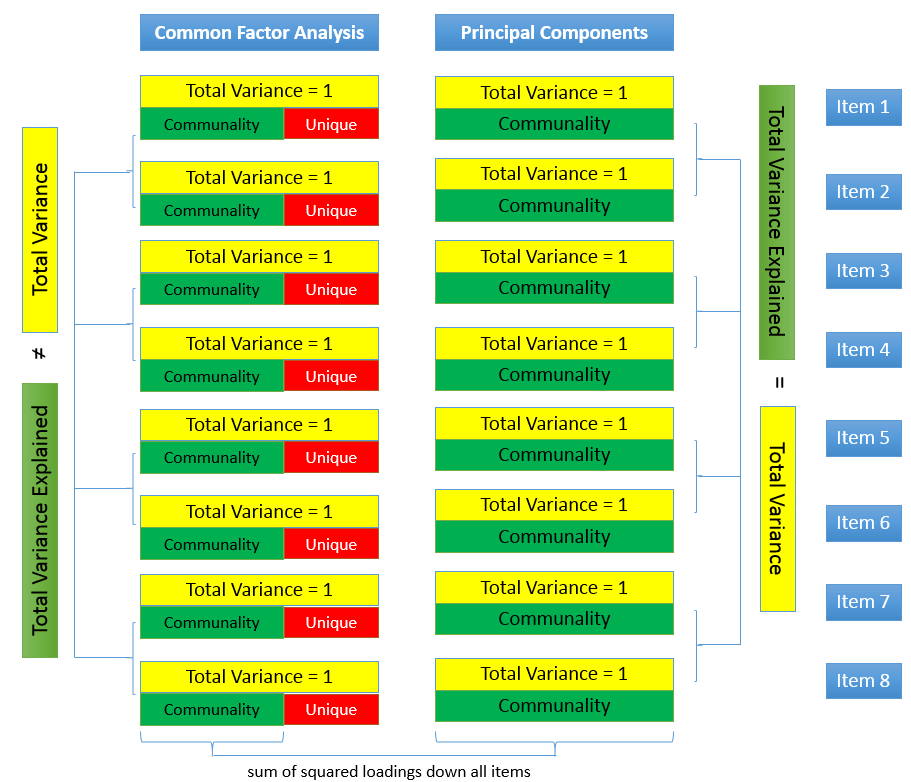
Common factor analysis
Common factor analysis
- Attempts to achieve parsimony (data reduction) by:
- Explaining the *maximum amount of common variance* in a correlation matrix
- Using the *smallest* number of explanatory constructs (factors)
- Explaining the *maximum amount of common variance* in a correlation matrix
- Attempts to achieve parsimony (data reduction) by:
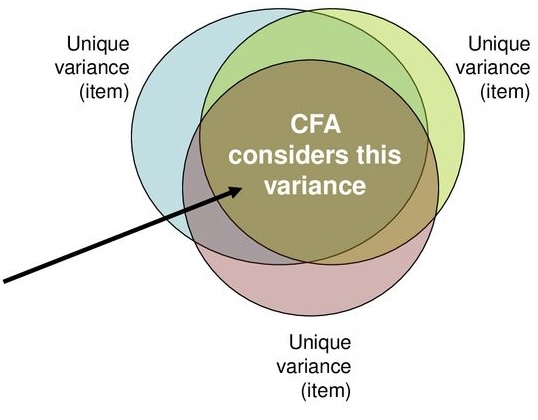
Common factor analysis
Partitions variance that is in common with other variables. How?
Use multiple regression
Each item as an outcome
Use all other items as predictors
Finds the communality among all of the variables, relative to one another
Common factor analysis
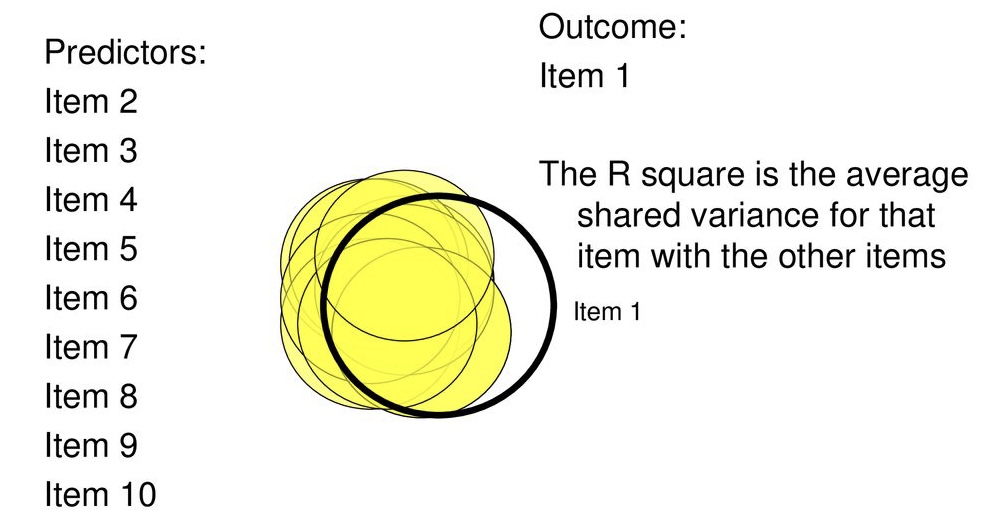
Common factor analysis
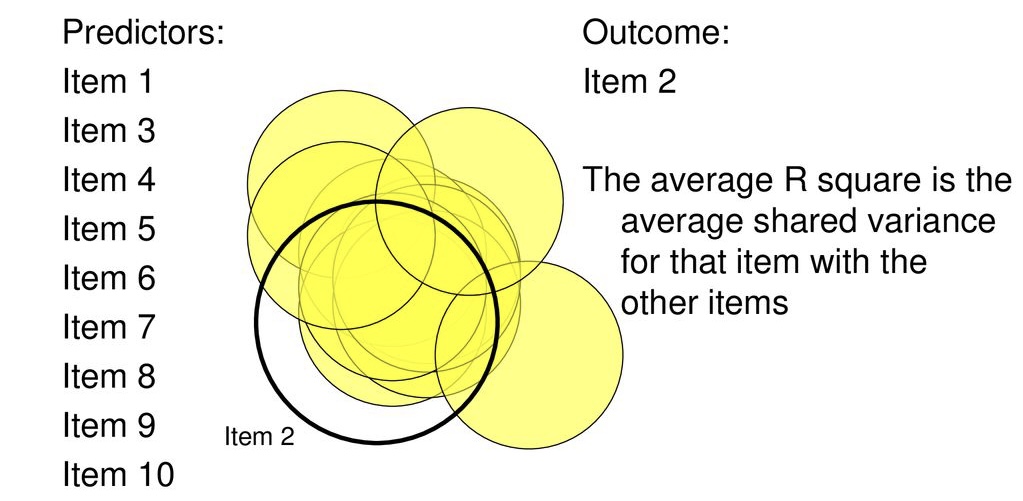
Common factor analysis
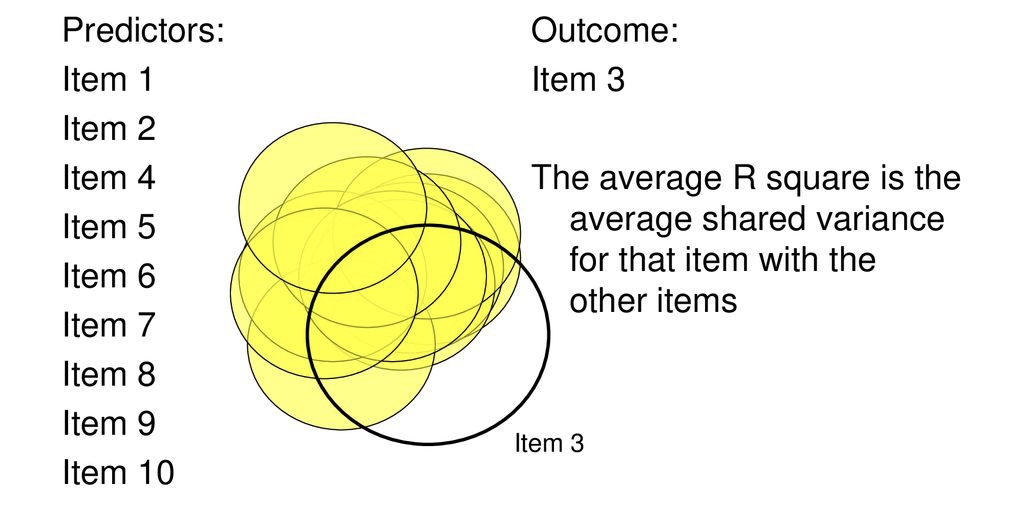
PCA
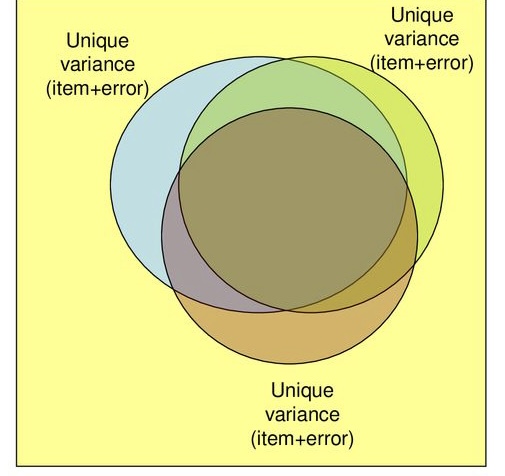
Assumption: Components that explain the most total variance
Goal: Find fewest components that account for the relationships among variables
PCA vs. FA
Run factor analysis if you assume or wish to test a theoretical model of latent factors causing observed variables
Run PCA If you want to simply reduce your correlated observed variables to a smaller set of important independent composite variables
Eigenvalues and Eigenvectors
Eigenvectors represent a weight for each eigenvalue
Eigenvector times the square root of the eigenvalue gives the factor loadings
- Correlation between item and factor
Eigenvalues represent the total amount of variance that can be explained by a given factor
- Sum of squared component loadings down all items for each factor
Factor analysis steps
Checking the suitability of data
Decide # of factors
Extraction
Rotation
Interpret/name
Data
Big 5
Big Five Personality Traits

Data visualization
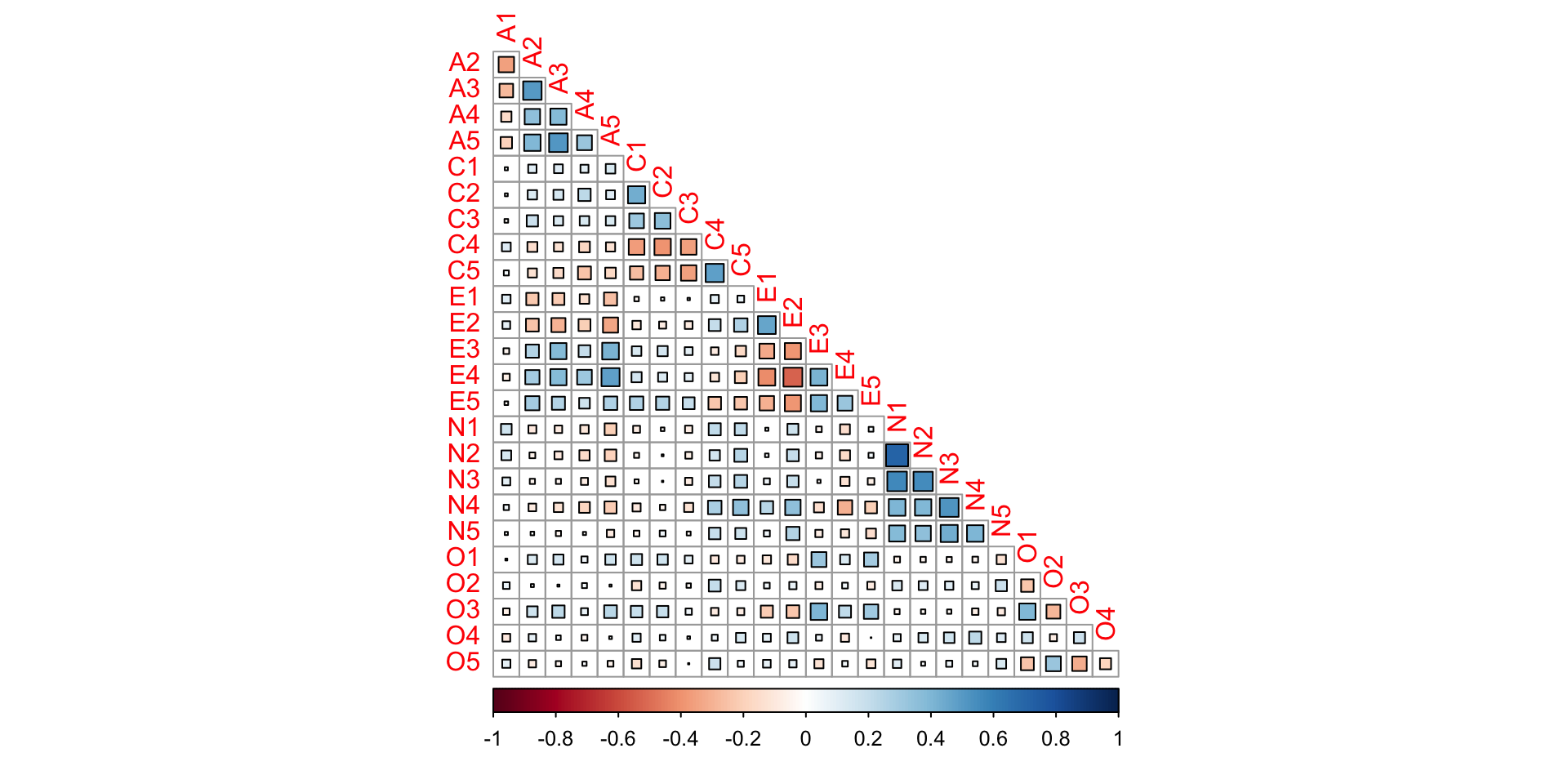
Is factor analysis warranted?
Bartlett’s test
Correlation matrix significantly different from identity matrix (0s)?
1 0 0 0 1 0 0 0 1
Is factor analysis warranted?
- Kaiser-Meyer-Olkin (KMO)
\[ KMO = \frac{\Sigma(r)^2}{\Sigma(r)^2 + \Sigma(r_p)^2} \]
Two variables share a common factor they will have small partial correlation (most of variance is explained by common factor so not much left)
KMO Criterion Adequacy Interpretation 0.00-0.49 Unacceptable 0.50-0.59 Poor 0.60-0.69 Fair 0.70-0.79 Good 0.80-0.89 Very Good 0.90-1.00 Excellent
Is factor analysis warranted?
# Is the data suitable for Factor Analysis?
- KMO: The Kaiser, Meyer, Olkin (KMO) measure of sampling adequacy suggests that data seems appropriate for factor analysis (KMO = 0.85).
- Sphericity: Bartlett's test of sphericity suggests that there is sufficient significant correlation in the data for factor analysis (Chisq(300) = 18146.07, p < .001). A1 A2 A3 A4 A5 C1 C2 C3
0.7540716 0.8364320 0.8702024 0.8780416 0.9035590 0.8433626 0.7958161 0.8519722
C4 C5 E1 E2 E3 E4 E5 N1
0.8265898 0.8641133 0.8381302 0.8838897 0.8970459 0.8774011 0.8933998 0.7794802
N2 N3 N4 N5 O1 O2 O3 O4
0.7803909 0.8623967 0.8852681 0.8602403 0.8586864 0.7803388 0.8444575 0.7701770
O5
0.7615938 Assumptions
No outliers
Large sample
- >100
Normality
No missingness
no multicolinerarity
Assumptions: Outliers
84 outliers detected: cases 31, 42, 149, 154, 170, 236, 285, 323, 357,
371, 397, 398, 416, 486, 488, 499, 579, 658, 693, 699, 724, 726, 753,
771, 773, 776, 840, 879, 880, 923, 992, 1002, 1012, 1056, 1078, 1111,
1116, 1127, 1131, 1155, 1243, 1255, 1277, 1309, 1310, 1313, 1316, 1359,
1363, 1364, 1368, 1369, 1370, 1371, 1435, 1500, 1537, 1541, 1558, 1677,
1685, 1738, 1775, 1786, 1797, 1815, 1816, 1865, 1906, 1933, 1936, 2018,
2186, 2194, 2257, 2259, 2263, 2272, 2314, 2315, 2346, 2393, 2398, 2413.
- Based on the following method and threshold: mahalanobis (52.62).
- For variables: A1, A2, A3, A4, A5, C1, C2, C3, C4, C5, E1, E2, E3, E4,
E5, N1, N2, N3, N4, N5, O1, O2, O3, O4, O5.Assumptions: Multicollinearity
We do not want variables that are too highly correlated
Determinant of correlation matrix
- Smaller < .00001 (close to 0) suggests a problem with multicollinearity
Fitting factor model: # of factors
Several different ways:
A priori
Eigenvalues > 1 (Kaiser criterion)
- New guideline: > .77
Cumulative percent variance extracted (75%)
Fitting factor model: # of factors
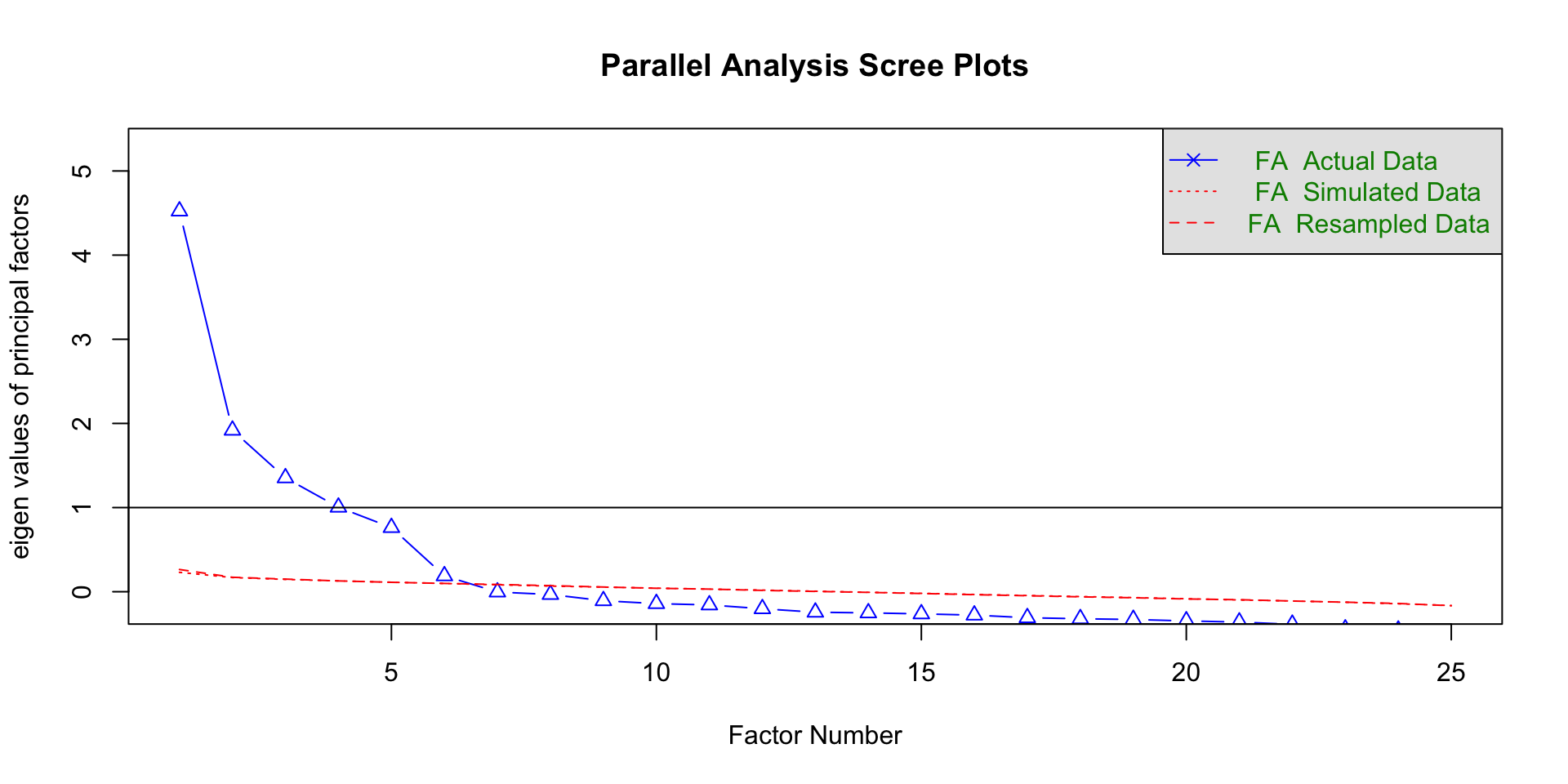
Scree plot
A plot of the Eigenvalues in order from largest to smallest
Look for the elbow (shared variability starting to level off)
- Above the elbow is how many components you want
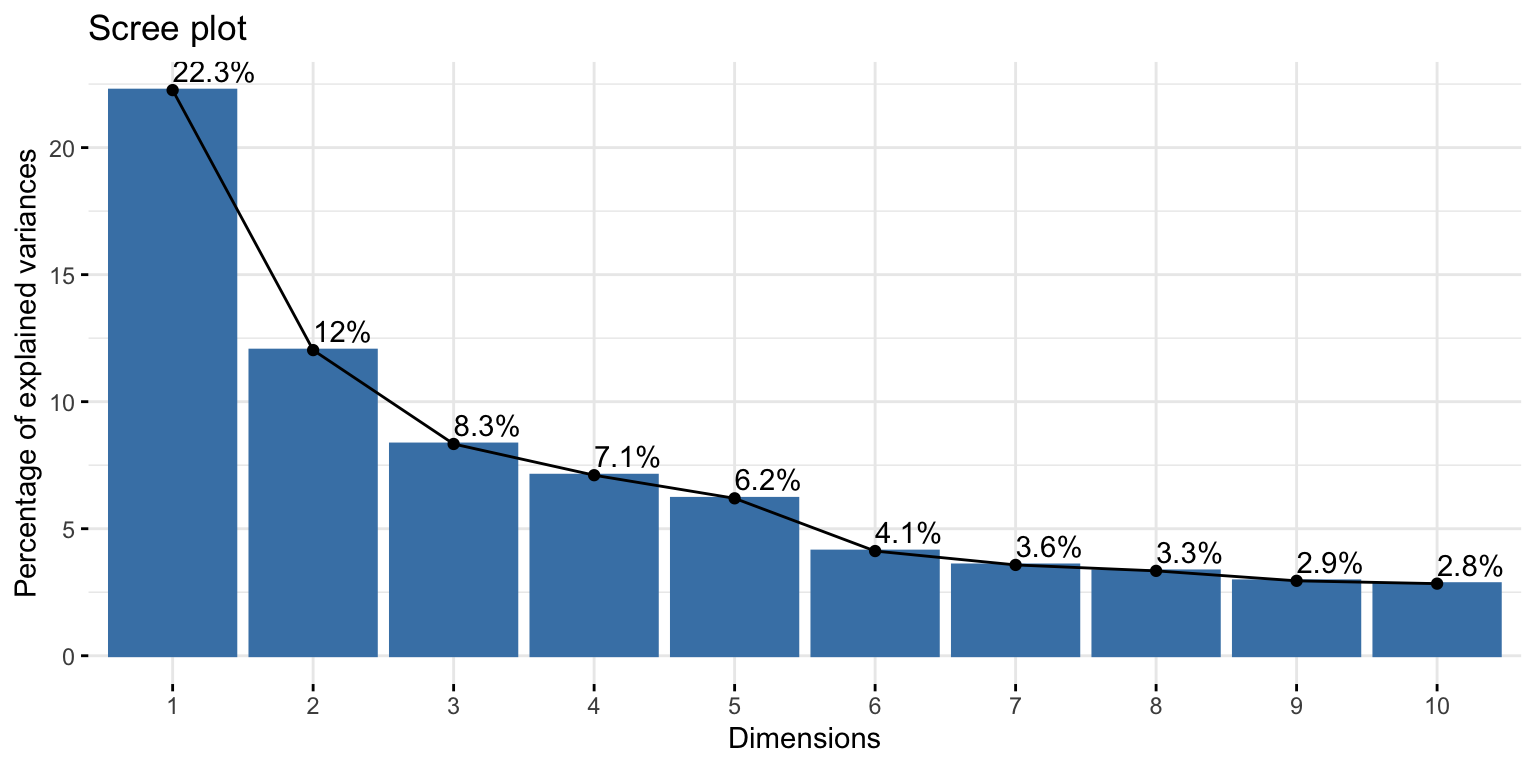
Fitting factor model: # of factors
Parallel analysis
Run simulations pulling eigenvalues from randomly generated datasets
If eigenvalues > eigenvalues from random datasets more likely to represent meaningful patterns in the data
More objective and reliable
Method agreement procedure
Uses many methods to determine how many factor you should get
- This is the approach I would use
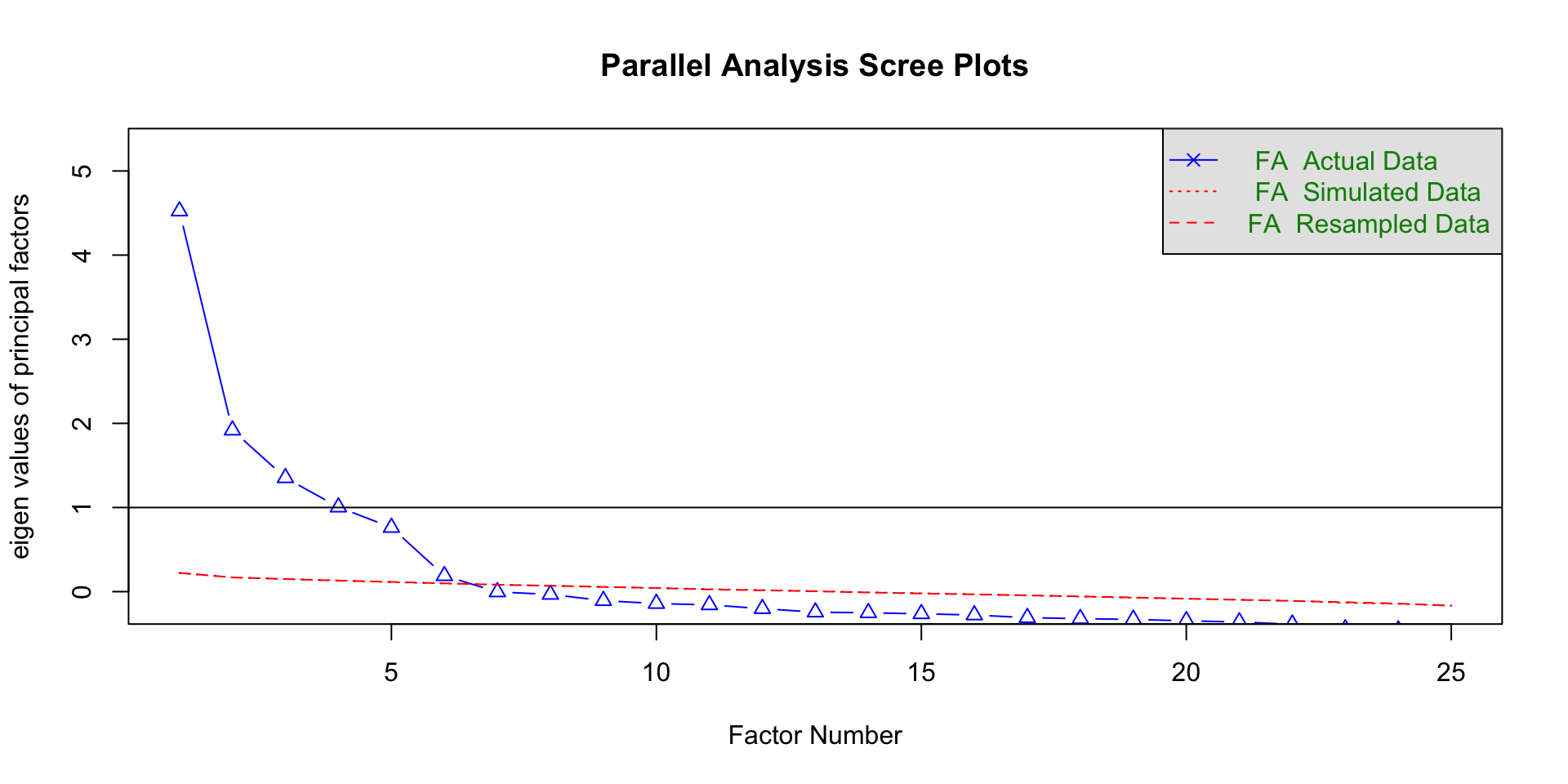
Extracting factor loadings
Once the number of factors are decided the researcher runs another factor analysis to get the loading for each of the factors
Principal axis factoring (PAF)
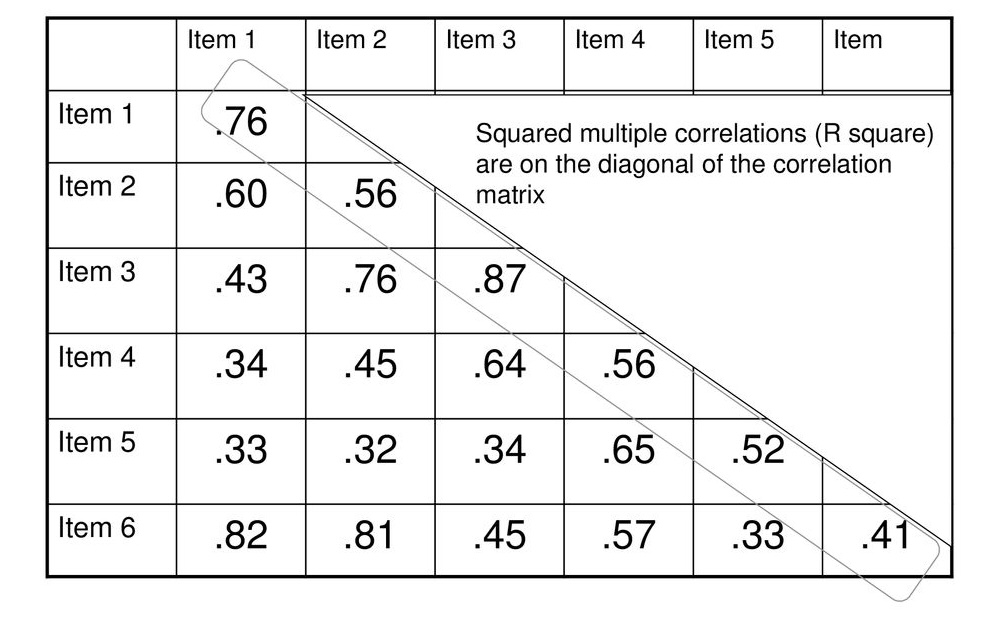
Get initial estimates of communalities
- Squared multiple correlations (highest absolute correlation)
Take correlation matrix and replace diagonal elements with communalities
Factor loadings
Correlation between item and factor
Naming: PA1-PA2…
- Reflects fitting method
- Factors ordered by variance explained
Loadings:
MR1 MR2 MR3 MR4 MR5
A1 -0.237 -0.132 -0.399
A2 0.481 0.275 0.205 0.350
A3 0.540 0.288 0.278 0.300
A4 0.416 0.111 0.141 0.249 0.185
A5 0.588 0.161 0.292 0.164
C1 0.353 0.149 -0.436 0.152
C2 0.343 0.220 -0.449 0.300
C3 0.329 -0.331 0.331
C4 -0.470 0.453 -0.239
C5 -0.504 0.122 0.277 -0.292
E1 -0.413 -0.178 -0.247 0.103 0.251
E2 -0.638 -0.212 0.322
E3 0.535 0.311 0.122 -0.181 -0.112
E4 0.606 0.159 0.352 -0.195
E5 0.524 0.293 -0.246
N1 -0.447 0.643 0.111 -0.247
N2 -0.436 0.629 -0.202
N3 -0.414 0.618
N4 -0.535 0.411 0.212
N5 -0.354 0.415 0.203 0.146
O1 0.333 0.210 -0.214 -0.366
O2 -0.191 0.335 0.355
O3 0.405 0.303 -0.166 -0.462
O4 0.257 -0.173 -0.255 0.302
O5 -0.212 0.304 0.409
MR1 MR2 MR3 MR4 MR5
SS loadings 4.762 2.276 1.600 1.266 0.994
Proportion Var 0.190 0.091 0.064 0.051 0.040
Cumulative Var 0.190 0.282 0.346 0.396 0.436Variance accounted for
| MR1 | MR2 | MR3 | MR4 | MR5 | |
|---|---|---|---|---|---|
| SS loadings | 4.7624190 | 2.2759454 | 1.5995842 | 1.2657972 | 0.9940470 |
| Proportion Var | 0.1904968 | 0.0910378 | 0.0639834 | 0.0506319 | 0.0397619 |
| Cumulative Var | 0.1904968 | 0.2815346 | 0.3455179 | 0.3961498 | 0.4359117 |
| Proportion Explained | 0.4370077 | 0.2088446 | 0.1467806 | 0.1161517 | 0.0912154 |
| Cumulative Proportion | 0.4370077 | 0.6458523 | 0.7926329 | 0.9087846 | 1.0000000 |
Path diagram
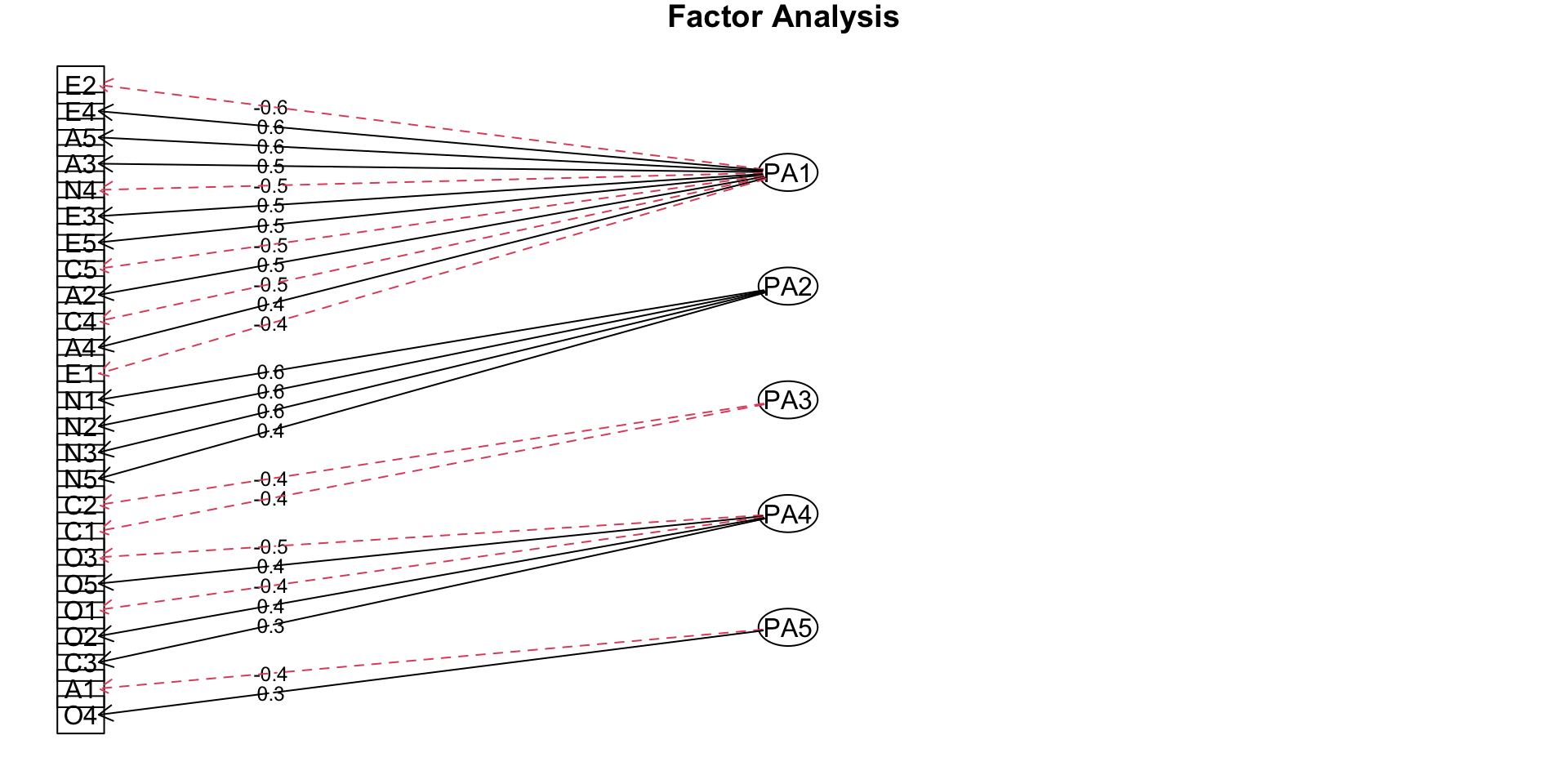
Rotation
Simple structure
Make more interpretable (understandable) without actually changing the relationships among the variables
- High factor loadings for each item on one factor
- Low factor loadings for all other factors
Rotation
Different types of rotation:
Orthogonal Rotation (e.g., Varimax)
This method of rotation prevents the factors from being correlated with each other
Useful if you have factors that should theoretically be unrelated
Oblique rotation (e.g., Direct Oblimin)
- Allows factors to correlate (more common)
- Good idea to always use this
Rotation
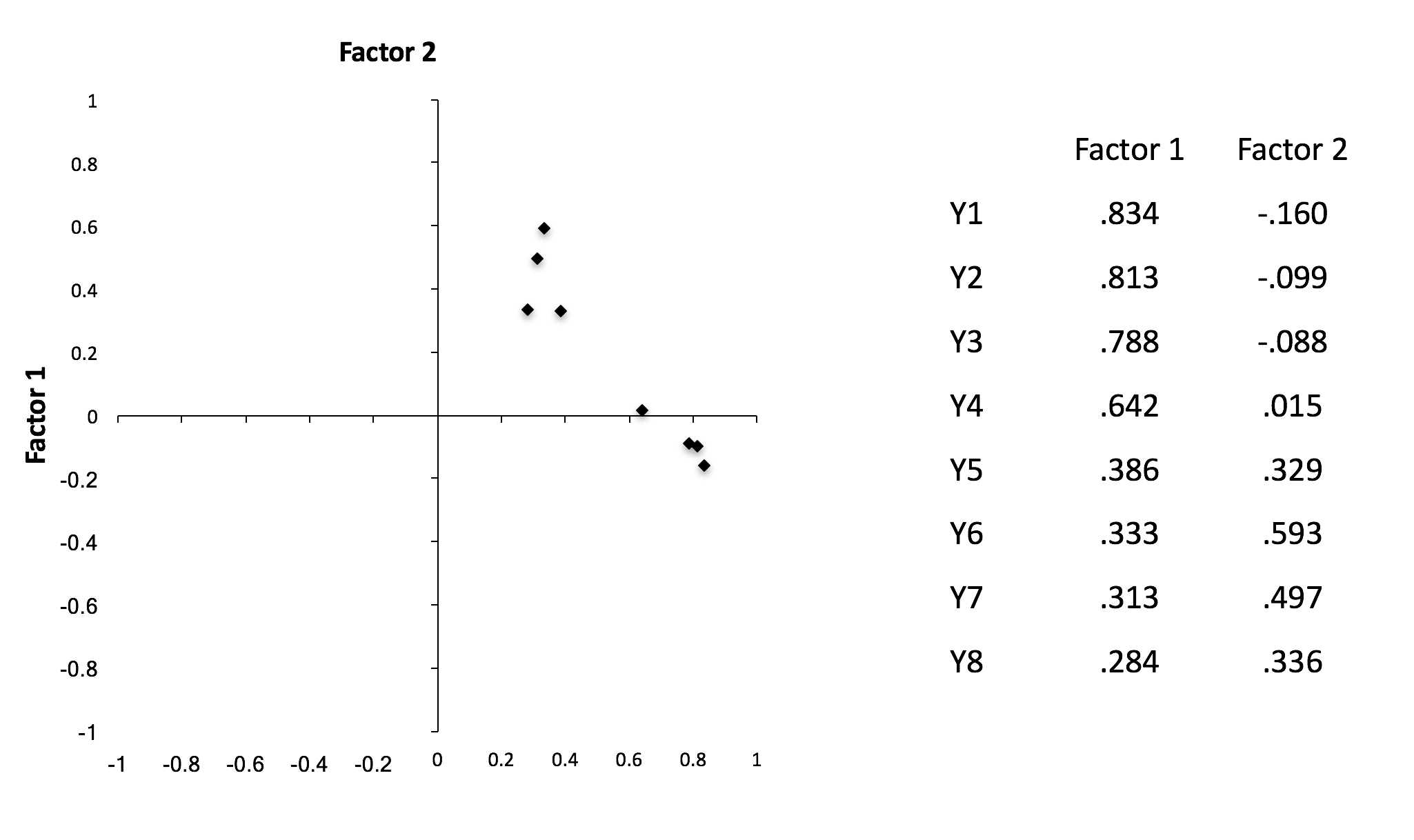
Rotation
- Orthogonal
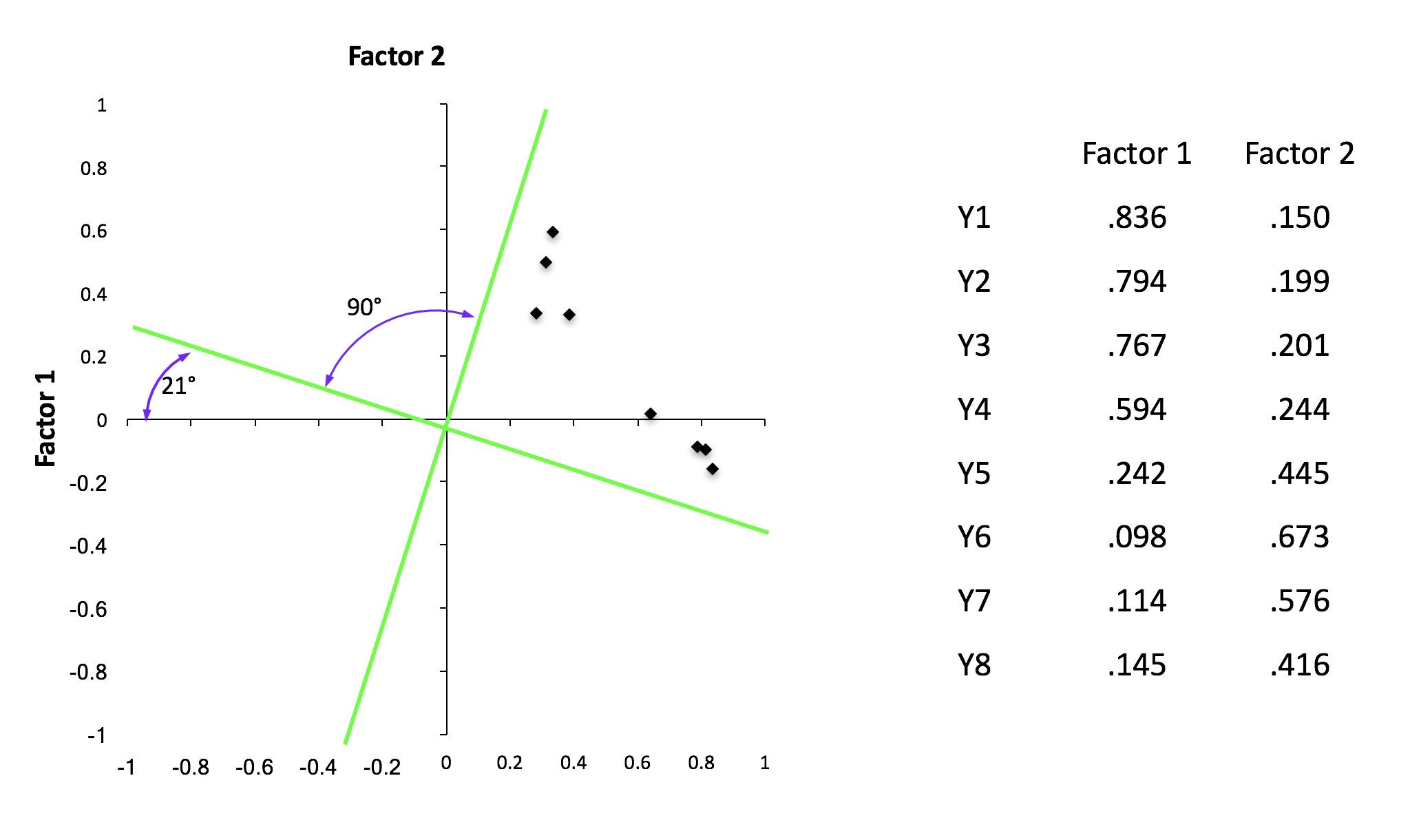
- Oblique
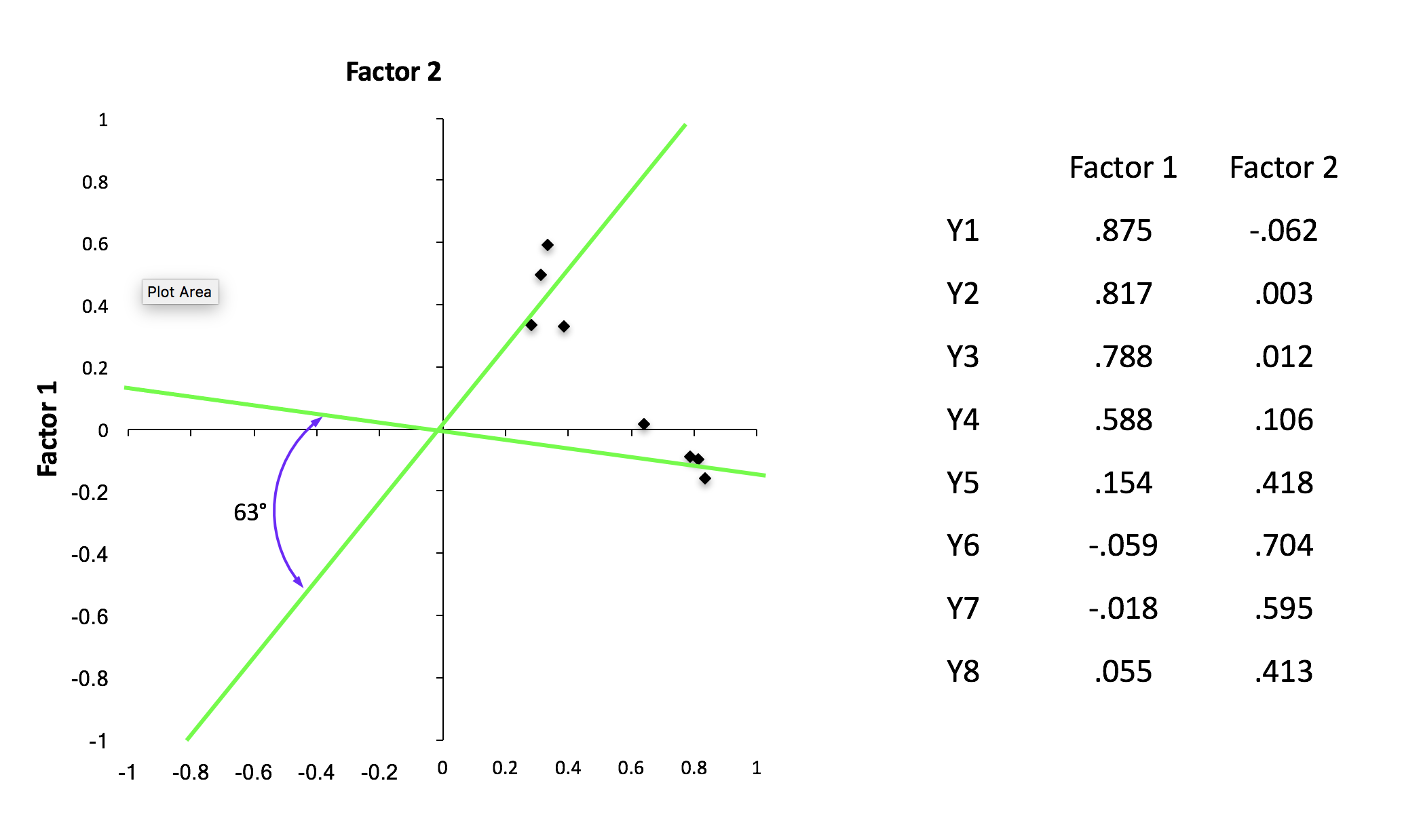
Rotation
Rotation
#change rotate arg to desired rotation
#orthogonal rotation
efa_or <- psych::fa(data, nfactors = 5, rotate="varimax", fm="pca") %>%
model_parameters(sort = TRUE, threshold = "max")
# correlated factor rotation
efa_obs <- psych::fa(data, nfactors = 5, rotate="oblimin", fm="pa") %>%
model_parameters(sort = TRUE, threshold = "max")Rotation
| Variable | PA2 | PA1 | PA3 | PA5 | PA4 | Complexity | Uniqueness |
|---|---|---|---|---|---|---|---|
| N1 | 0.8328843 | NA | NA | NA | NA | 1.068333 | 0.3130370 |
| N2 | 0.7950692 | NA | NA | NA | NA | 1.042690 | 0.3649887 |
| N3 | 0.7136687 | NA | NA | NA | NA | 1.086772 | 0.4424073 |
| N5 | 0.4947880 | NA | NA | NA | NA | 2.020818 | 0.6357309 |
| N4 | 0.4846713 | NA | NA | NA | NA | 2.261132 | 0.4937518 |
| E2 | NA | -0.6656809 | NA | NA | NA | 1.106647 | 0.4409754 |
| E4 | NA | 0.6109409 | NA | NA | NA | 1.459828 | 0.4378787 |
| E1 | NA | -0.5390781 | NA | NA | NA | 1.235679 | 0.6634869 |
| E5 | NA | 0.4417103 | NA | NA | NA | 2.517237 | 0.5699586 |
| E3 | NA | 0.4312233 | NA | NA | NA | 2.446913 | 0.5562281 |
| C2 | NA | NA | 0.6762158 | NA | NA | 1.164003 | 0.5396502 |
| C4 | NA | NA | -0.6564115 | NA | NA | 1.119814 | 0.5116338 |
| C3 | NA | NA | 0.5863922 | NA | NA | 1.088822 | 0.6647049 |
| C1 | NA | NA | 0.5688726 | NA | NA | 1.163902 | 0.6399189 |
| C5 | NA | NA | -0.5619399 | NA | NA | 1.413916 | 0.5625583 |
| A3 | NA | NA | NA | 0.6732427 | NA | 1.076716 | 0.4536902 |
| A2 | NA | NA | NA | 0.6580435 | NA | 1.036931 | 0.5203702 |
| A5 | NA | NA | NA | 0.5337231 | NA | 1.559262 | 0.5158711 |
| A1 | NA | NA | NA | -0.4599196 | NA | 1.886162 | 0.7654362 |
| A4 | NA | NA | NA | 0.4418032 | NA | 1.788660 | 0.6981428 |
| O3 | NA | NA | NA | NA | 0.6378560 | 1.171308 | 0.5031688 |
| O5 | NA | NA | NA | NA | -0.5536560 | 1.211116 | 0.6819619 |
| O1 | NA | NA | NA | NA | 0.5314361 | 1.121555 | 0.6646212 |
| O2 | NA | NA | NA | NA | -0.4797808 | 1.692361 | 0.7204800 |
| O4 | NA | NA | NA | NA | 0.3675394 | 2.737417 | 0.7419059 |
Rotation
- After rotation
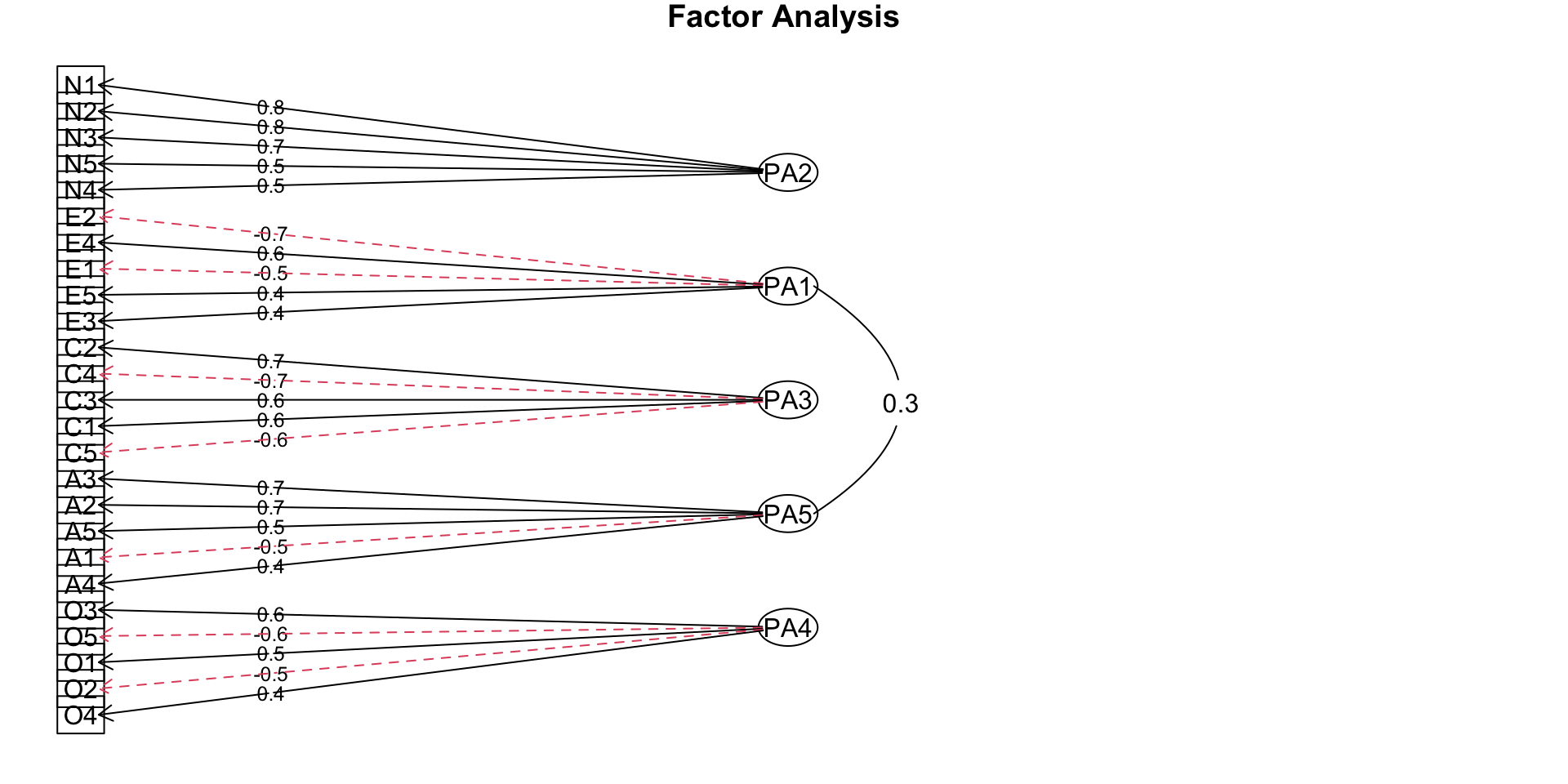
What makes a good factor?
Makes sense
- Loadings on the same factor do not appear to measure completely different things
Easy to interpret
Simple structure
- Contains either high or low loadings with few moderately sized loadings
- Lacks cross-loadings
- You don’t have items that load equally onto more than 1 factor
- Keep items > .3 and delete items < .3
- You don’t have items that load equally onto more than 1 factor
3 or more indicators per latent factor
Factor scores
Estimated scores for each participant on each underlying factor (standing on factor)
Standardize the factor loadings by dividing each loading by the square root of the sum of squares of the factor loading for that factor.
Multiply scores on each item by the corresponding standardized factor loading and then summing across all items.
Can use them in multiple regression!
Factor scores
Geller, J., Thye, M., & Mirman, D. (2019). Estimating effects of graded white matter damage and binary tract disconnection on post-stroke language impairment. NeuroImage, 189. https://doi.org/10.1016/j.neuroimage.2019.01.020
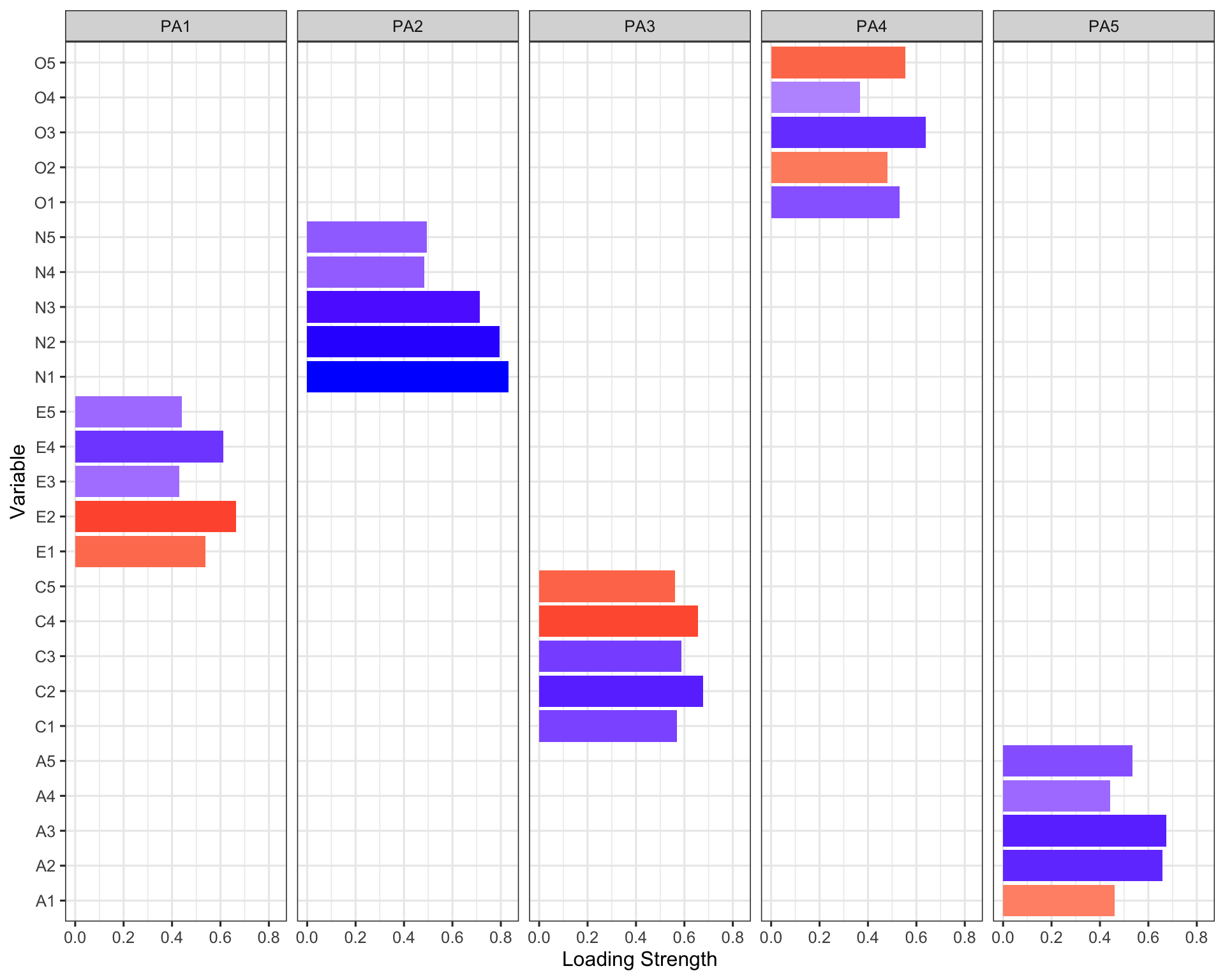
Plotting FA
# correlated rotation
efa_obs <- psych::fa(data, nfactors = 5, rotate="oblimin", fm="pa") %>%
model_parameters(sort = TRUE, threshold = "max")
efa_plot <- as.data.frame(efa_obs) %>%
pivot_longer(PA2:PA4) %>%
dplyr::select(-Complexity, -Uniqueness) %>% rename("Loadings" = value, "Personality" = name)
#For each test, plot the loading as length and fill color of a bar
# note that the length will be the absolute value of the loading but the
# fill color will be the signed value, more on this below
efa_fact_plot <- ggplot(efa_plot, aes(Variable, abs(Loadings), fill=Loadings)) +
facet_wrap(~ Personality, nrow=1) + #place the factors in separate facets
geom_bar(stat="identity") + #make the bars
coord_flip() + #flip the axes so the test names can be horizontal
#define the fill color gradient: blue=positive, red=negative
scale_fill_gradient2(name = "Loading",
high = "blue", mid = "white", low = "red",
midpoint=0, guide=F) +
ylab("Loading Strength") + #improve y-axis label
theme_bw(base_size=12) #use a black-and0white theme with set font sizeTable FA
FA table
| Factor analysis results | ||||||||
| Factor_1 | Factor_2 | Factor_3 | Factor_4 | Factor_5 | Communality | Uniqueness | Complexity | |
|---|---|---|---|---|---|---|---|---|
| N1 | 0.833 | 0.100 | 0.002 | -0.109 | -0.041 | 0.69 | 0.31 | 1.07 |
| N2 | 0.795 | 0.041 | 0.012 | -0.106 | 0.022 | 0.64 | 0.36 | 1.04 |
| N3 | 0.714 | -0.108 | -0.034 | 0.094 | 0.013 | 0.56 | 0.44 | 1.09 |
| N5 | 0.495 | -0.209 | -0.001 | 0.213 | -0.166 | 0.36 | 0.64 | 2.02 |
| N4 | 0.485 | -0.394 | -0.135 | 0.099 | 0.080 | 0.51 | 0.49 | 2.26 |
| E2 | 0.110 | -0.666 | -0.033 | -0.066 | -0.076 | 0.56 | 0.44 | 1.11 |
| E4 | -0.009 | 0.611 | 0.010 | 0.290 | -0.071 | 0.56 | 0.44 | 1.46 |
| E1 | -0.055 | -0.539 | 0.094 | -0.101 | -0.105 | 0.34 | 0.66 | 1.24 |
| E5 | 0.157 | 0.442 | 0.282 | 0.039 | 0.206 | 0.43 | 0.57 | 2.52 |
| E3 | 0.080 | 0.431 | 0.004 | 0.230 | 0.292 | 0.44 | 0.56 | 2.45 |
| C2 | 0.150 | -0.080 | 0.676 | 0.080 | 0.036 | 0.46 | 0.54 | 1.16 |
| C4 | 0.150 | 0.011 | -0.656 | 0.038 | -0.041 | 0.49 | 0.51 | 1.12 |
| C3 | 0.036 | -0.042 | 0.586 | 0.078 | -0.077 | 0.34 | 0.66 | 1.09 |
| C1 | 0.062 | -0.039 | 0.569 | 0.005 | 0.144 | 0.36 | 0.64 | 1.16 |
| C5 | 0.182 | -0.147 | -0.562 | 0.019 | 0.088 | 0.44 | 0.56 | 1.41 |
| A3 | -0.018 | 0.122 | 0.033 | 0.673 | 0.031 | 0.55 | 0.45 | 1.08 |
| A2 | -0.015 | 0.017 | 0.081 | 0.658 | 0.029 | 0.48 | 0.52 | 1.04 |
| A5 | -0.119 | 0.256 | 0.002 | 0.534 | 0.032 | 0.48 | 0.52 | 1.56 |
| A1 | 0.210 | 0.195 | 0.058 | -0.460 | -0.066 | 0.23 | 0.77 | 1.89 |
| A4 | -0.053 | 0.084 | 0.198 | 0.442 | -0.155 | 0.30 | 0.70 | 1.79 |
| O3 | 0.041 | 0.163 | -0.001 | 0.079 | 0.638 | 0.50 | 0.50 | 1.17 |
| O5 | 0.122 | 0.113 | -0.048 | 0.041 | -0.554 | 0.32 | 0.68 | 1.21 |
| O1 | 0.012 | 0.113 | 0.065 | 0.000 | 0.531 | 0.34 | 0.66 | 1.12 |
| O2 | 0.190 | 0.102 | -0.090 | 0.141 | -0.480 | 0.28 | 0.72 | 1.69 |
| O4 | 0.122 | -0.342 | -0.037 | 0.183 | 0.368 | 0.26 | 0.74 | 2.74 |
Confirmatory factor analysis
Do not do a confirmatory analysis with the same data you performed your exploratory analysis!
- Machine learning approach
Partition data training and test data
CFA in Lavaan
Let’s compare the big6 to the big5
structure_big5 <- psych::fa(training, nfactors = 5, rotate = "oblimin") %>%
efa_to_cfa()
# Investigate how the models look
structure_big5# Latent variables
MR2 =~ N1 + N2 + N3 + N4 + N5
MR1 =~ E1 + E2 + E3 + E4 + E5
MR3 =~ C1 + C2 + C3 + C4 + C5
MR5 =~ A1 + A2 + A3 + A4 + A5 + .row_id
MR4 =~ O1 + O2 + O3 + O4 + O5CFA in Lavaan
Fit and compare models
big5 <- suppressWarnings(lavaan::cfa(structure_big5, data = test))
big6 <- suppressWarnings(lavaan::cfa(structure_big6, data = test))
performance::compare_performance(big5, big6, verbose = FALSE)| Name | Model | Chi2 | Chi2_df | p_Chi2 | Baseline | Baseline_df | p_Baseline | GFI | AGFI | NFI | NNFI | CFI | RMSEA | RMSEA_CI_low | RMSEA_CI_high | p_RMSEA | RMR | SRMR | RFI | PNFI | IFI | RNI | Loglikelihood | AIC | AIC_wt | BIC | BIC_wt | BIC_adjusted |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| big5 | lavaan | 1.42e+03 | 289 | 0 | 5.57e+03 | 325 | 0 | 0.849 | 0.816 | 0.744 | 0.757 | 0.784 | 0.0746 | 0.0707 | 0.0785 | 3.84e-14 | 11.8 | 0.0764 | 0.713 | 0.662 | 0.785 | 0.784 | -3.4e+04 | 6.81e+04 | 1 | 6.84e+04 | 1 | 6.82e+04 |
| big6 | lavaan | 1.56e+03 | 289 | 0 | 5.57e+03 | 325 | 0 | 0.839 | 0.804 | 0.721 | 0.729 | 0.759 | 0.0788 | 0.075 | 0.0826 | 0 | 11.7 | 0.0842 | 0.686 | 0.641 | 0.76 | 0.759 | -3.41e+04 | 6.82e+04 | 3.31e-29 | 6.85e+04 | 3.31e-29 | 6.83e+04 |
Information to include in paper

Write-up
Factorablity
KMO
Bartlett’s test
Determinant of correlation matrix
Number of components
Scree plot
Eigenvalues > .77
Parallel analysis
Agreement method
Type of rotation
- PAF or PCA
Factor loadings
- Place in table or figure
Sample write-up
First, data were screened to determine the suitability of the data for this analyses. The Kaiser-Meyer- Olkin measure of sampling adequacy (KMO; Kaiser, 1970) represents the ratio of the squared correlation between variables to the squared partial correlation between variables. KMO ranges from 0.00 to 1.00 – values closer to 1.00 indicate that the patterns of correlations are relatively compact and that component analysis should yield distinct and reliable components (Field, 2012). In our dataset, the KMO value was .86, indicating acceptable sampling adequacy. The Barlett’s Test of Sphericity examines whether the population correlation matrix resembles an identity matrix (Field, 2012). When the p value for the Bartlett’s test is < .05, we are fairly certain we have clusters of correlated variables. In our dataset, χ1(300)=1683.76,p<.001, indicating the correlations between items are sufficiently large enough for principal components analysis. The determinant of the correlation matrix alerts us to any issues of multicollinearity or singularity and should be larger than 0.00001. Our determinant was 0.00115 and, again, indicated that our data was suitable for the analysis.
Sample write-up
Several criteria were used to determine the number of components to extract: a priori theory, the scree test, the eigenvalue-greater-than-one criteria, and the interpretability of the solution. Kaiser’s eigenvalue-greater-than-one criteria suggested four components, and, in combination explained 49% of the variance. The inflexion (elbow) in the scree plot justified retaining four components. Based on the convergence of these decisions, four components were extracted. We investigated each with orthogonal (varimax) and oblique (oblimin) procedures. Given the non-significant correlations (ranging from -0.03 to 0.03) and the clear component loadings in the orthogonal rotation, we determined that an orthogonal solution was most appropriate.
More resources
Added two new articles to website
Work through Kabacoff, R. I. (2022). *R* in Action* Chapter 14
PSY 504: Advanced Statistics