Mediation Analysis in R
Princeton University
3/27/23
Today
Classical approach to testing mediation (Baron and Kenny)
Bootstrapped approach to testing mediation (preferred approach)
Other models:
Multiple mediators
Within-subject mediation
Mediation: Example
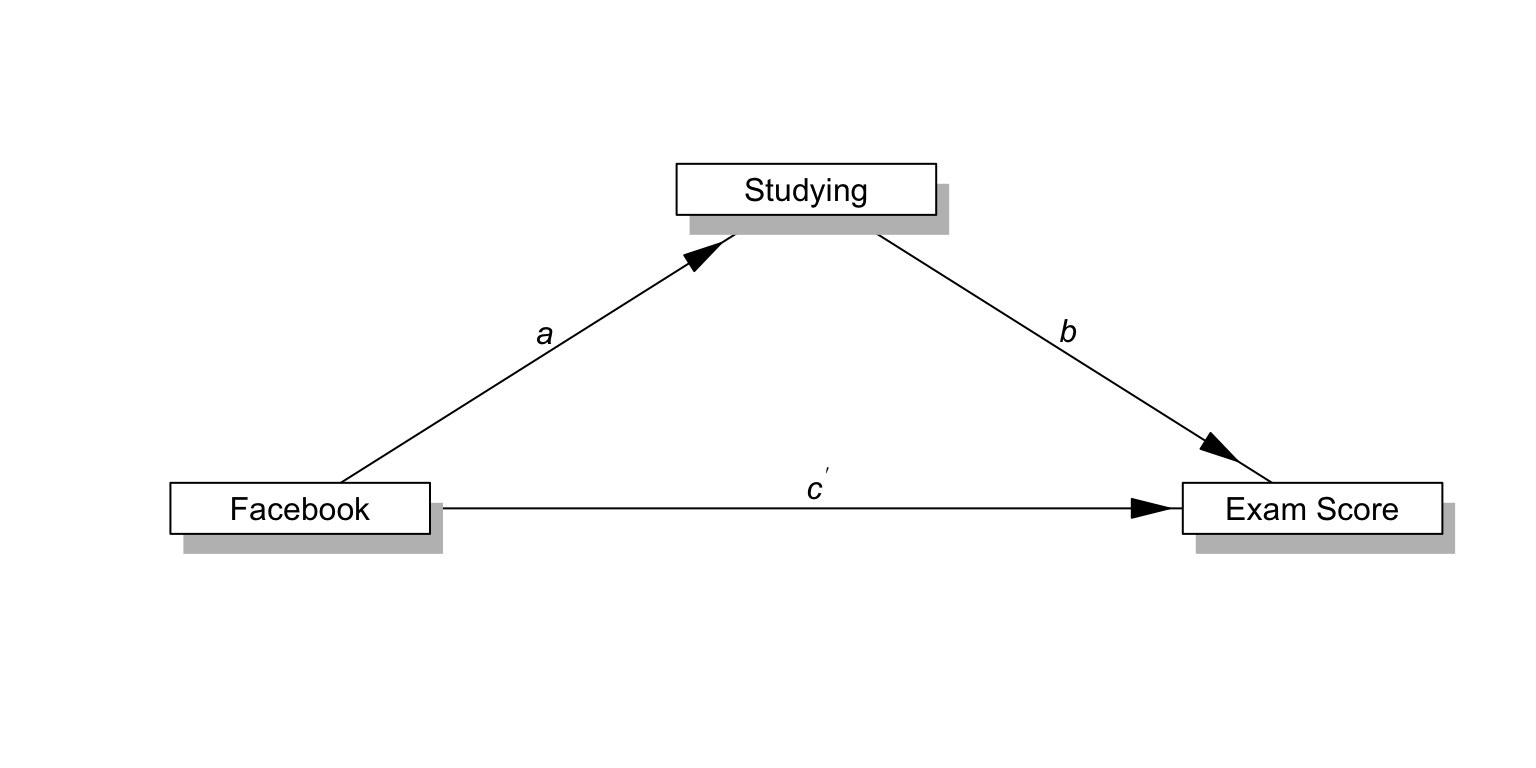
Does study time mediate the relationship between Facebook usage and exam scores?
- Implying that the overuse of Facebook prevents people from studying, so they do differently on their exam
![]()
Load packages
Load data
Classical approach - Baron & Kenny
- Mediation is tested through three regression models:
- Predicting the mediator from the predictor variable
- X -> Y
- c: total path
Predicting the outcome from the predictor variable
X -> M
a path
Predicting the outcome from both the predictor variable and the mediator
X+M→Y
b path
c’ (c-prime) path
Classical approach - Baron & Kenny (1986)
Traditionally, to show mediation ALL these conditions must be met:
X must significantly predict Y in Step 1
X must significantly predict M in Step 2
M must significantly predict Y controlling for X in Step 3
The effect of X on Y must be reduced in Step 4
If X is no longer significant, you have “full mediation”
If X is still significant, then you have “partial mediation”
Mediation: c path
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 4.57 | 0.539 | 8.48 | 2.5e-15 |
| -0.661 | 0.128 | -5.16 | 5.15e-07 |
The c path (total effect): X --> Y:
\(b = -0.66, t(237) = -5.16, p < .001\)
Mediation: a path
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 2.45 | 0.41 | 5.97 | 8.43e-09 |
| -0.211 | 0.0973 | -2.17 | 0.0313 |
The a path: X --> M:
\(b = -0.21, t(237) = -2.16, p = .031\)
Mediation: b, c’ path
Add in the b (M –> Y) and c’ (direct) paths: X + M --> Y
c’ Path: \(b = -0.61, t(237) = -4.77, p < .001\)
b Path: \(b = 0.26, t(237) = 3.09, p = .002\)
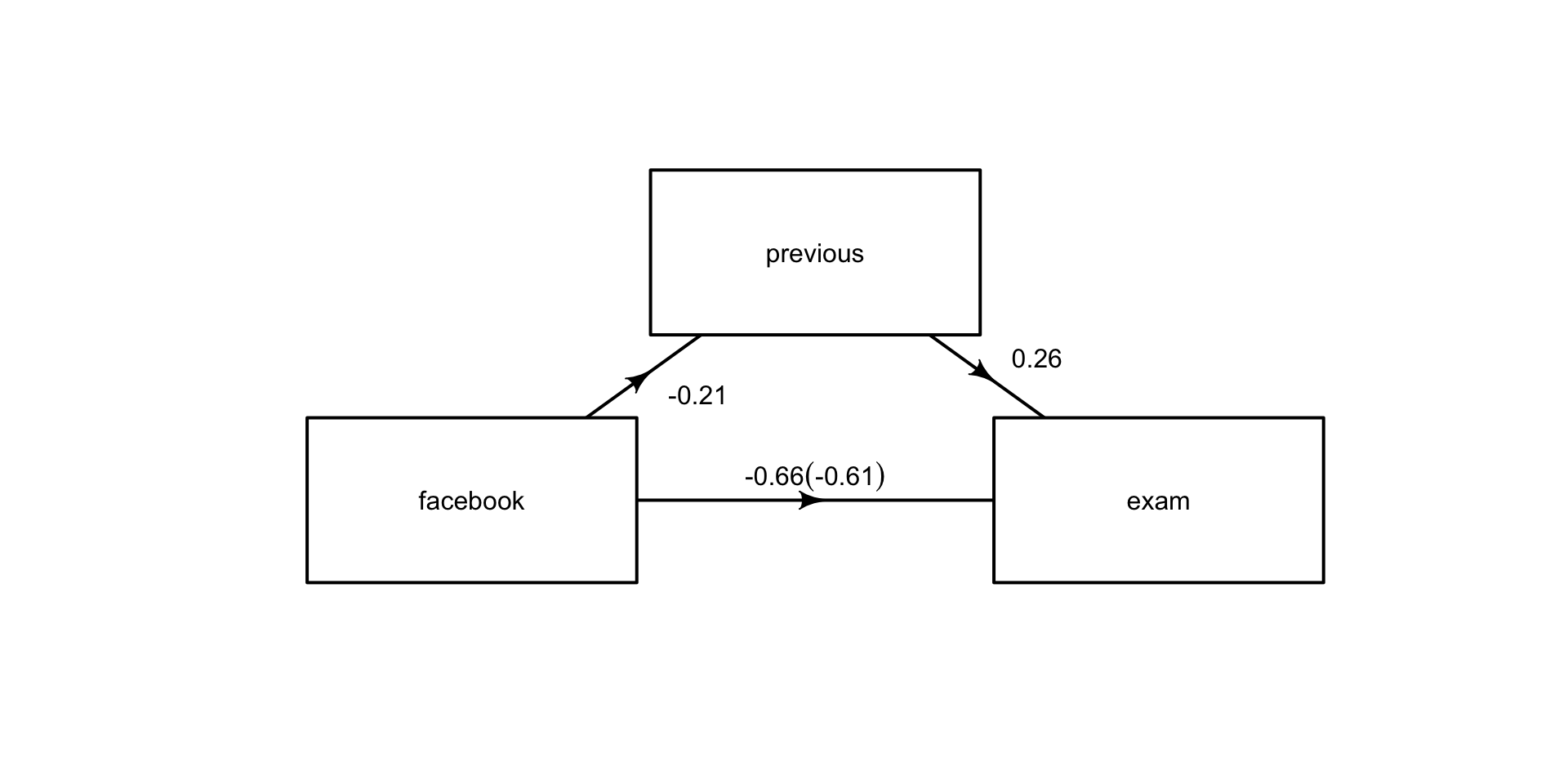
Mediation: interpretation
Facebook usage negatively impacts exam scores (c path = -.66)
Facebook time negatively impacts previous study time (a path = -.21)
Controlling for Facebook time, previous experience positively impacts exam scores (b path = .26)
Controlling for previous studying, Facebook time negatively impacts exam scores (c’ path = -0.61)
Testing mediation: Sobel test
So, did mediation happen? Is a change from 0.66 to 0.61 important?
The Aroian Test:
\[Z = \frac{a \times b}{\sqrt{b^2 \times SE_a^2 + a^2 \times SE_b^2 + SE_a^2 \times SE_b^2}}\]
- If the indirect effect is larger than the error, we would conclude that the addition of the M variable changed the c path.
Aroian Test
Aroian test
| Sobel | Aroian | Goodman |
|---|---|---|
| -1.77 | -1.71 | -1.84 |
| 0.0761 | 0.0864 | 0.0658 |
Z = -1.71, p = .09
- We would conclude that no mediation had occurred.
Sobel test
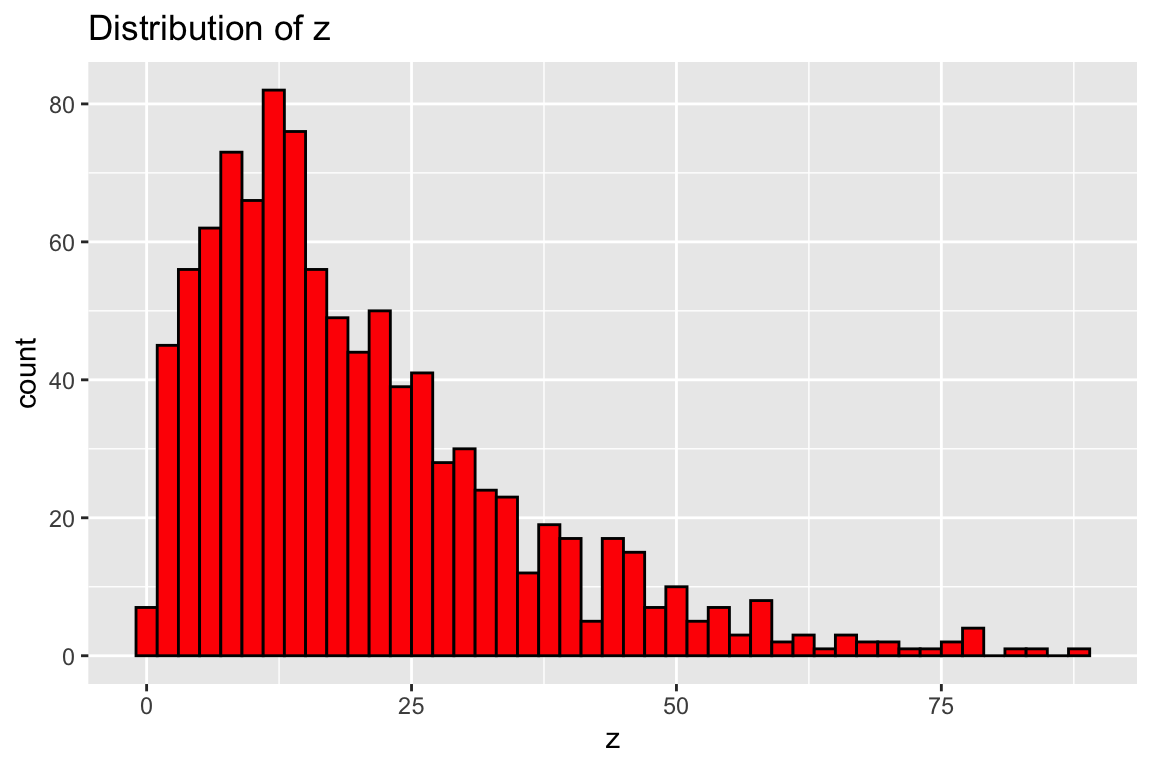
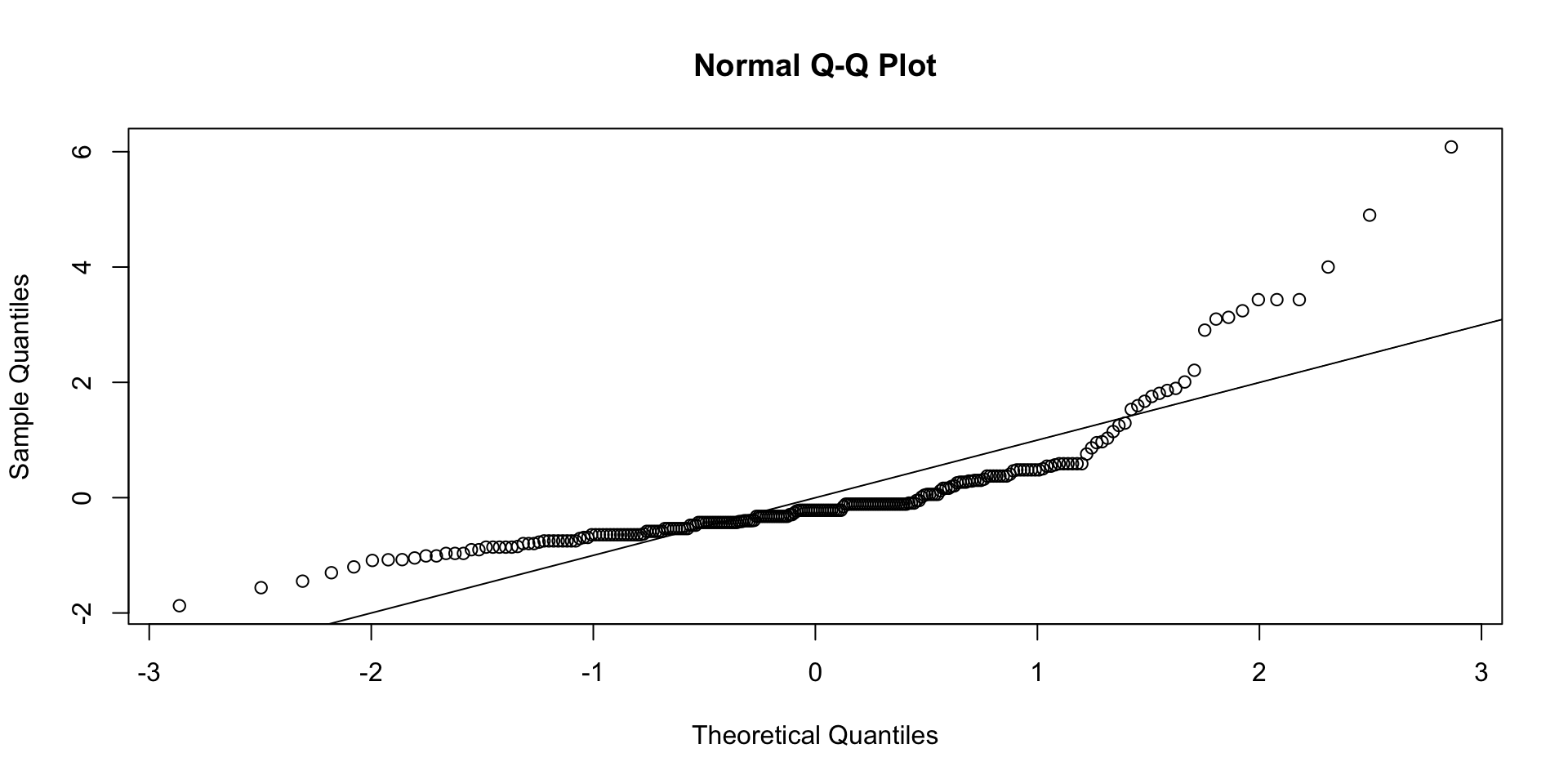
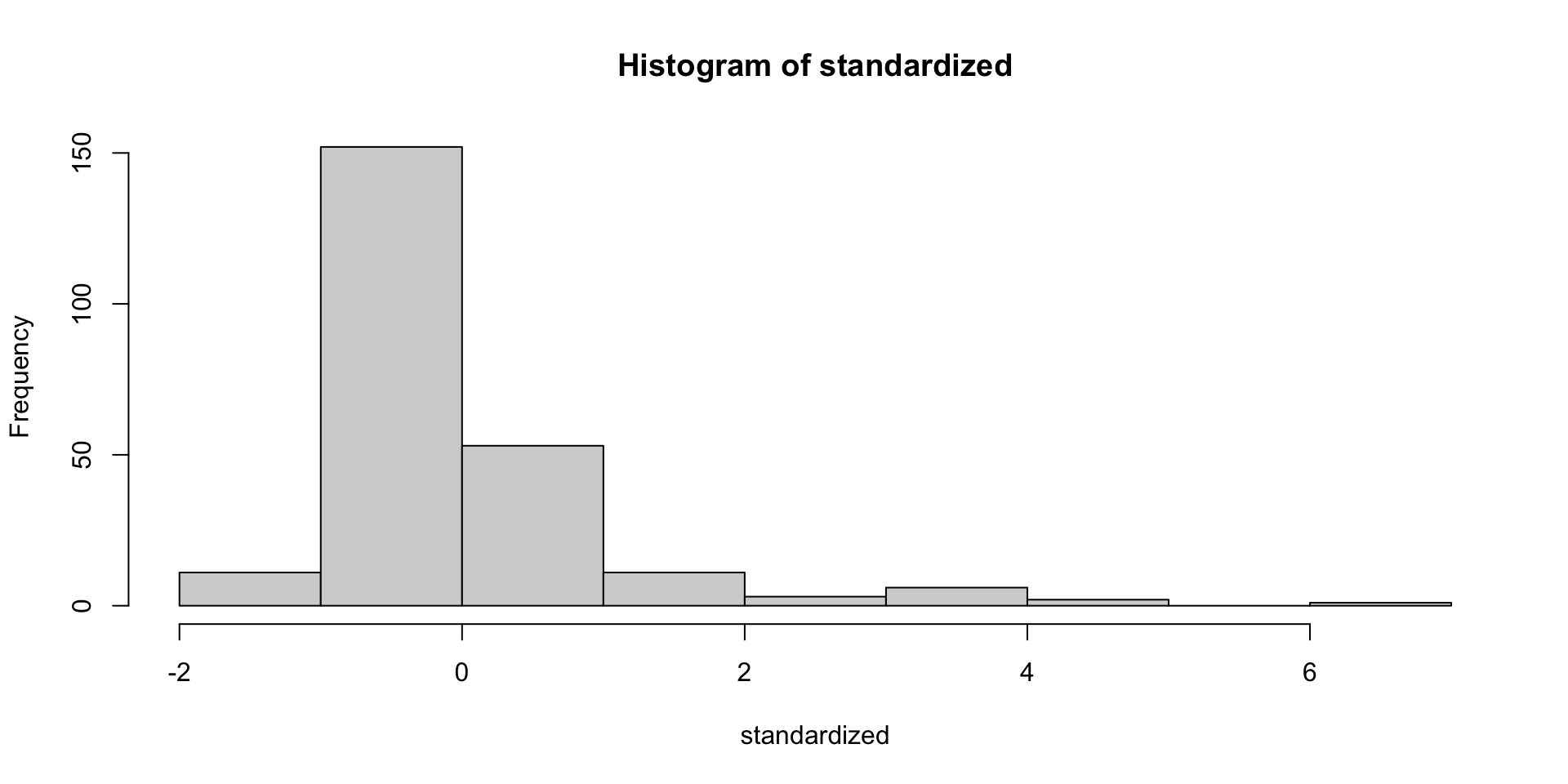
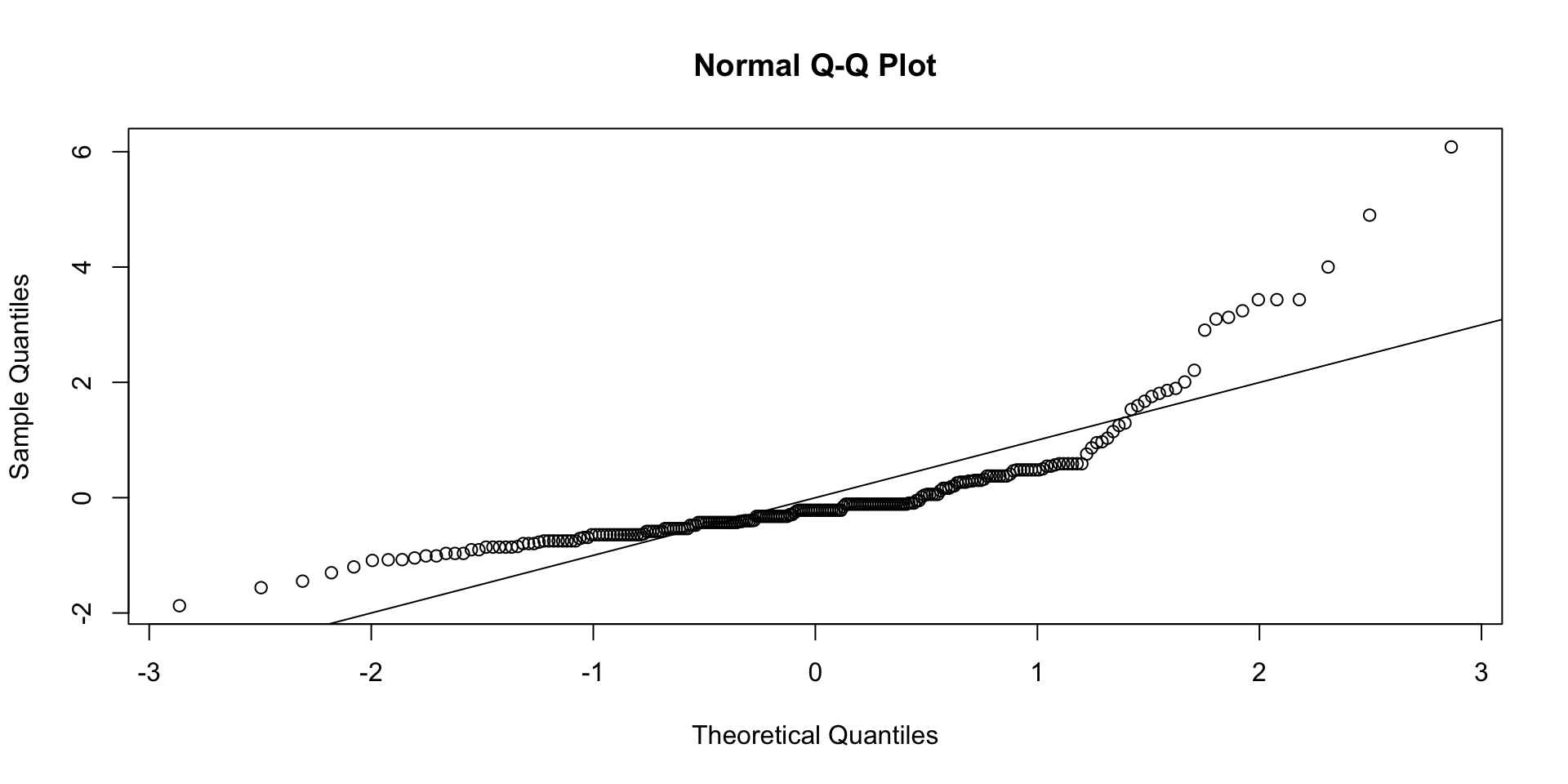
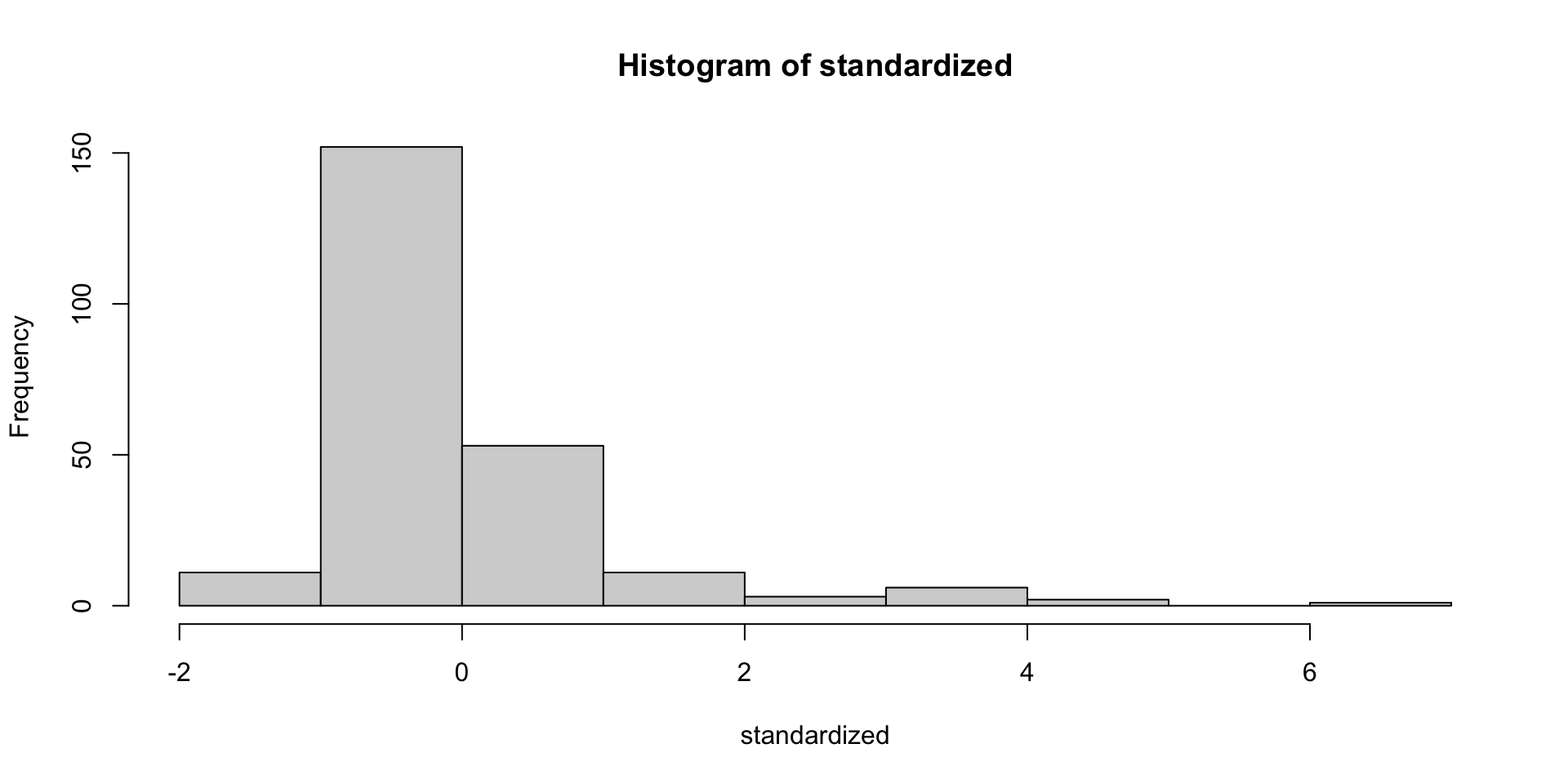
- Assumes indirect effect is normally distributed
It is not!
- It is skewed and leptokurtic
Mediation: Bootstrapping
Testing significance of indirect effect (a x b)
- Does not assume distribution is normal
- More sensitive test = Higher power!
Bias corrected and accelerated (Bca) bootstrap confidence intervals
- Bias-correction
\[\begin{align*} \hat{z}_0 &= \Phi^{-1}\Bigg(\frac{1}{B}\sum_i \hat{\theta}^*_i < \hat\theta \Bigg) \end{align*}\]
Bias Corrected and Accelerated (Bca) bootstrap confidence intervals
Skew
- Jacknifing
\[\begin{align*} \hat{a} &= \frac{\sum_i (\bar{\theta}^{-i} - \hat{\theta}^{-i} )^3 }{6 \cdot \big[\sum_i (\bar{\theta}^{-i} - \hat{\theta}^{-i} )^2 \big]^{3/2}} \end{align*}\]
Mediation: All together + bootstrapping
Mediation: MeMoBoot
The MeMoBootR package (developed by Erin Buchanon) gives you data screening, each step of the mediation, and the bootstrapping results!
- The data screening does not include accuracy or missing data, so that should be completed first.
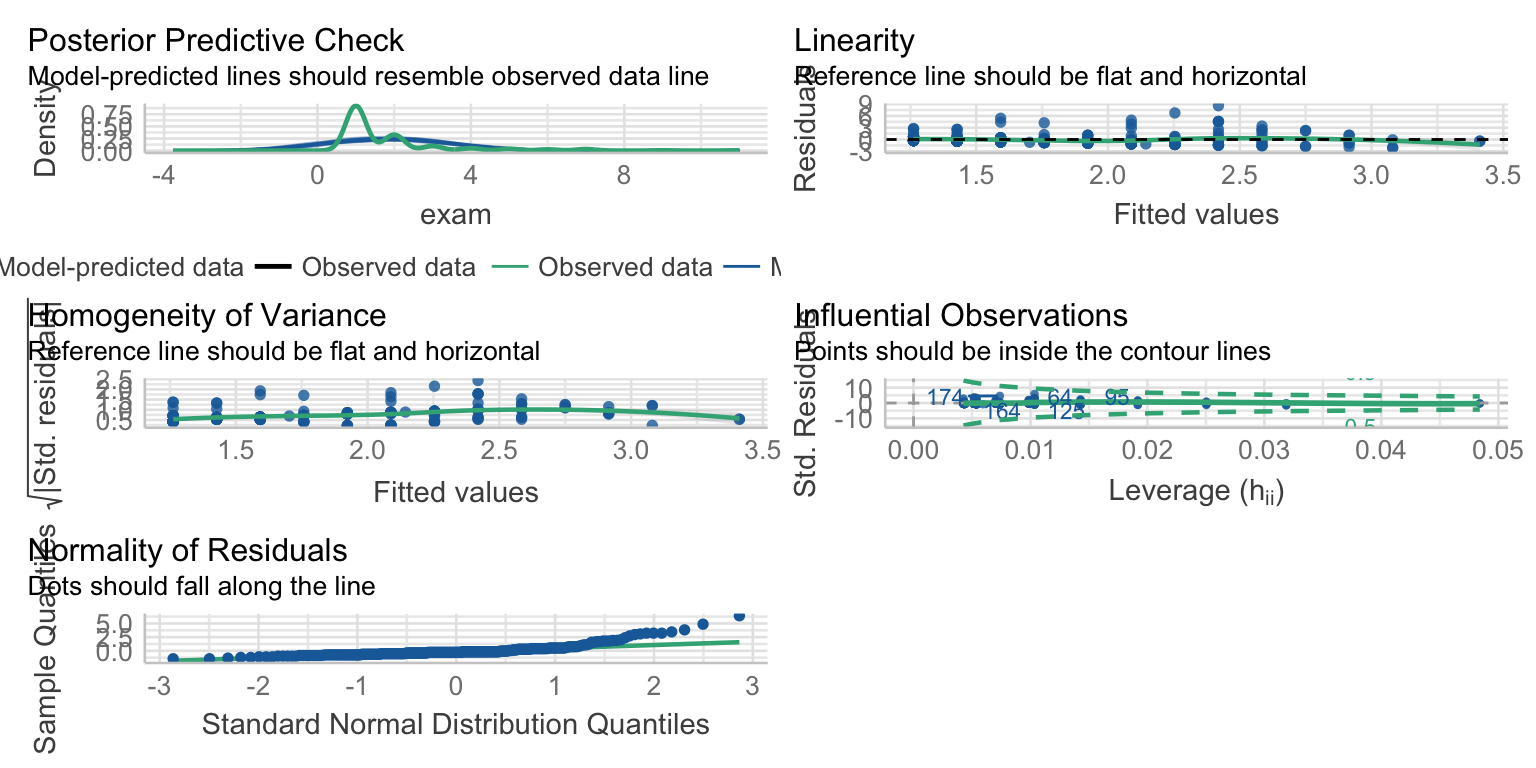
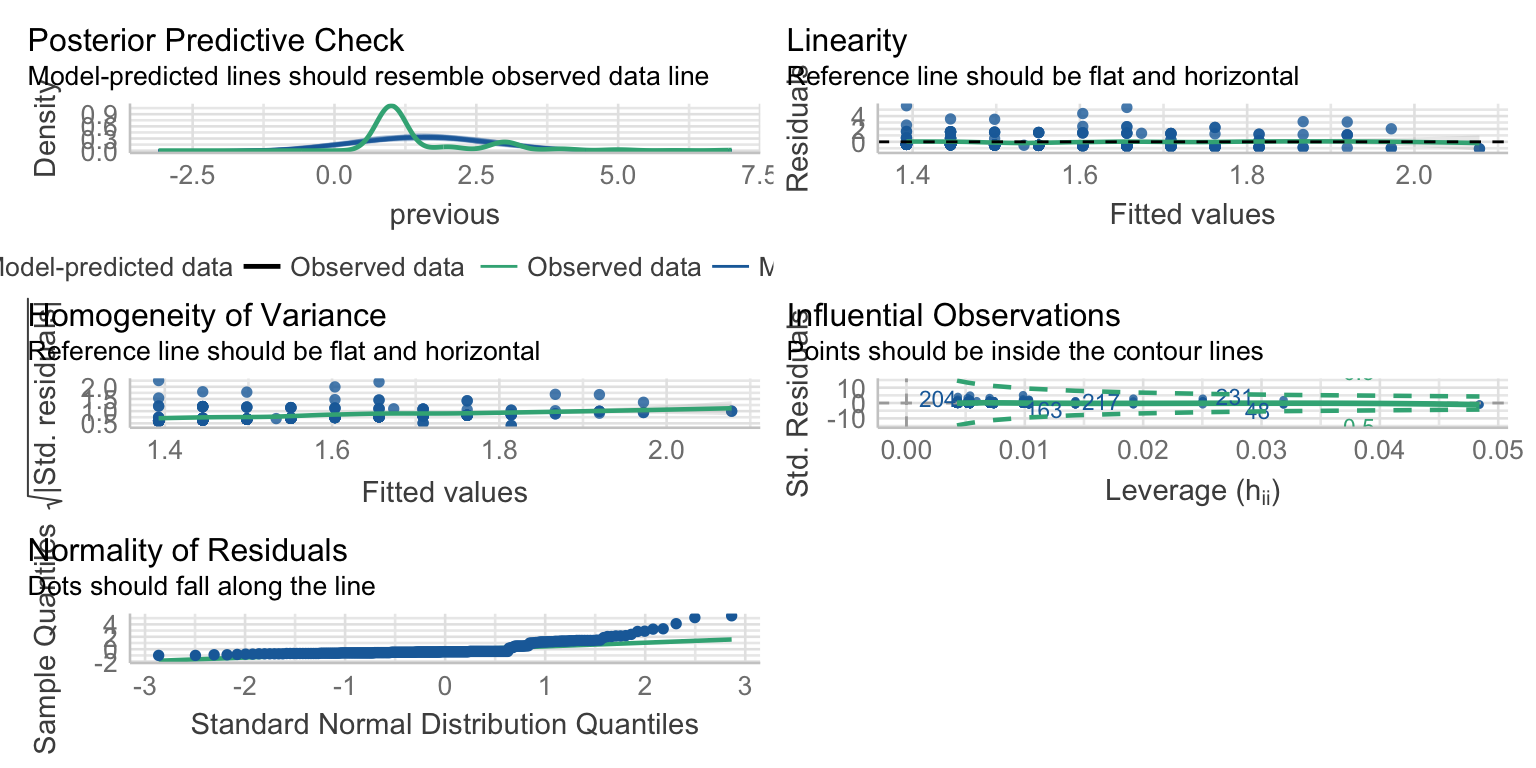
Assumptions
Mediation: MeMoBootR
For each of our stages of mediation, you can print out the models:
Mediation: MeMoBootR
- Next, you can get the Sobel test results:
Bootstrapping
Last, let’s get the bootstrapped results:
The indirect effect would be reported as: $0.05, 95\% CI[-0.1782, -0.0067 ]$
Returns normal cis (adding bca)
Bootstrapping
Mediation visualization
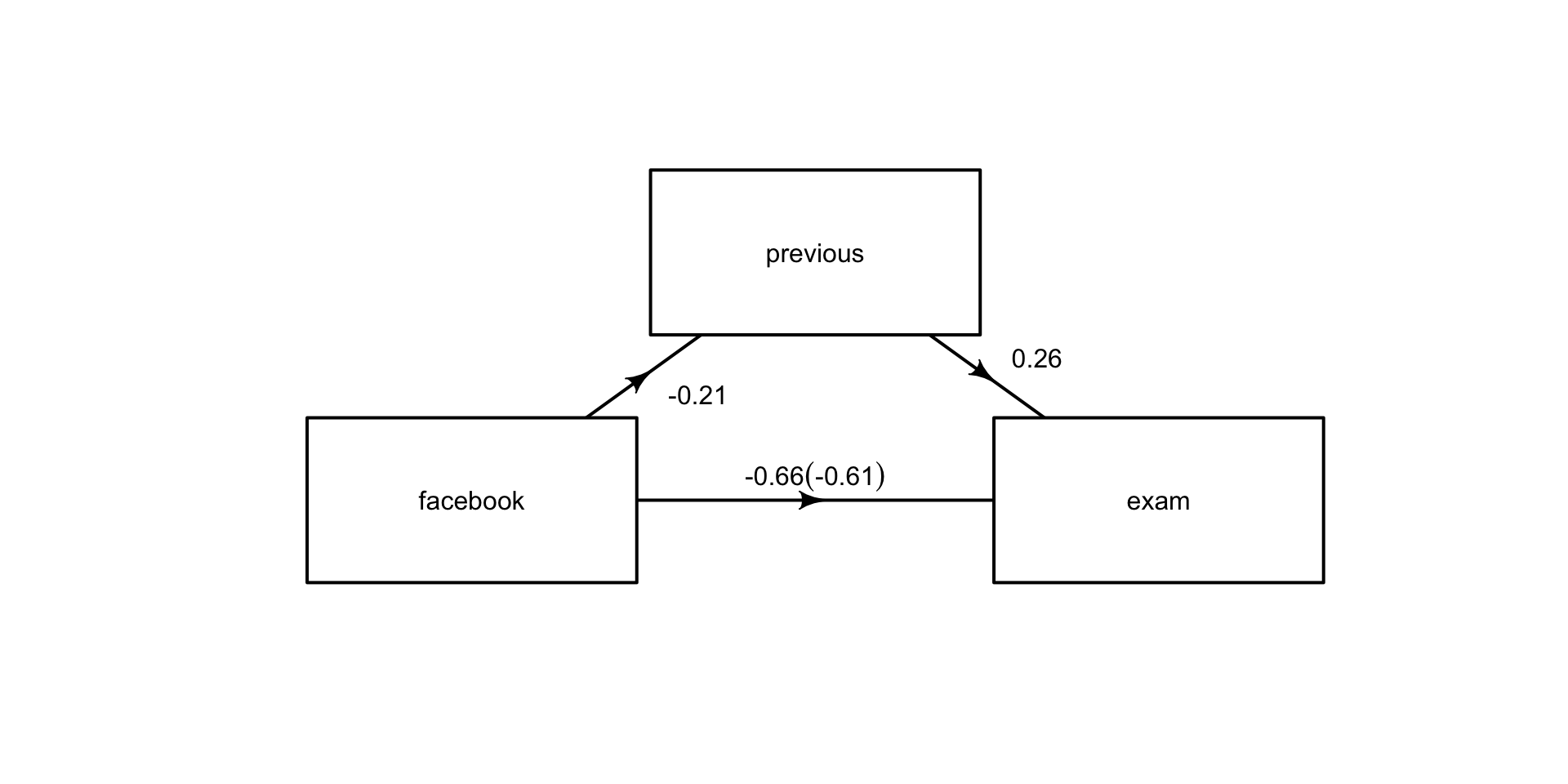
Mediation visualization
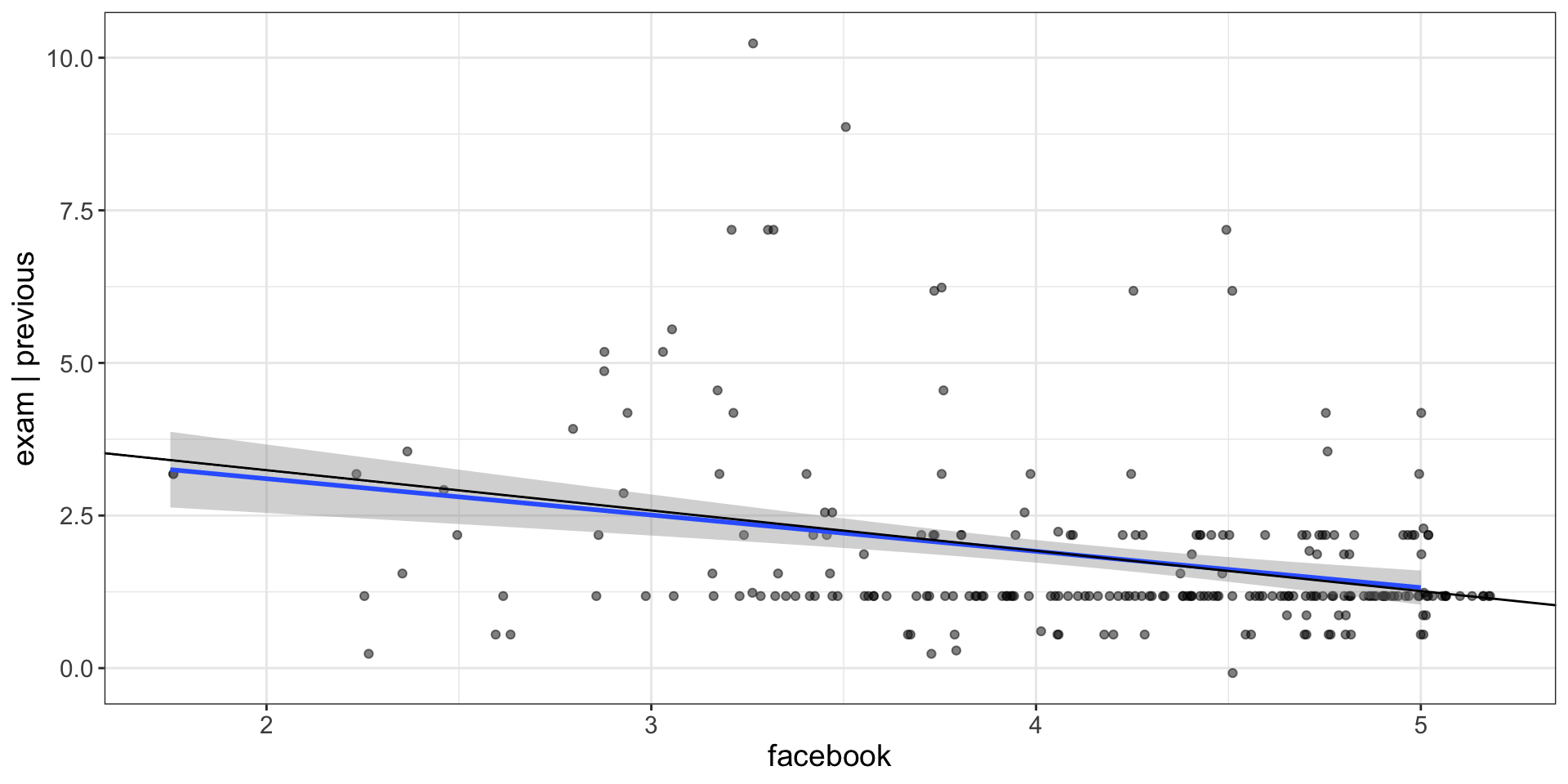
JSmediation
Incorporates
easystats
JSmediation results
Test of mediation (simple mediation)
==============================================
Variables:
- IV: facebook
- DV: exam
- M: previous
Paths:
==== ============== ===== =======================
Path Point estimate SE APA
==== ============== ===== =======================
a -0.211 0.097 t(237) = 2.17, p = .031
b 0.260 0.084 t(236) = 3.09, p = .002
c -0.661 0.128 t(237) = 5.16, p < .001
c' -0.606 0.127 t(236) = 4.77, p < .001
==== ============== ===== =======================
Indirect effect index:
Indirect effect index is not computed by default.
Please use add_index() to compute it.
Fitted models:
- X -> Y
- X -> M
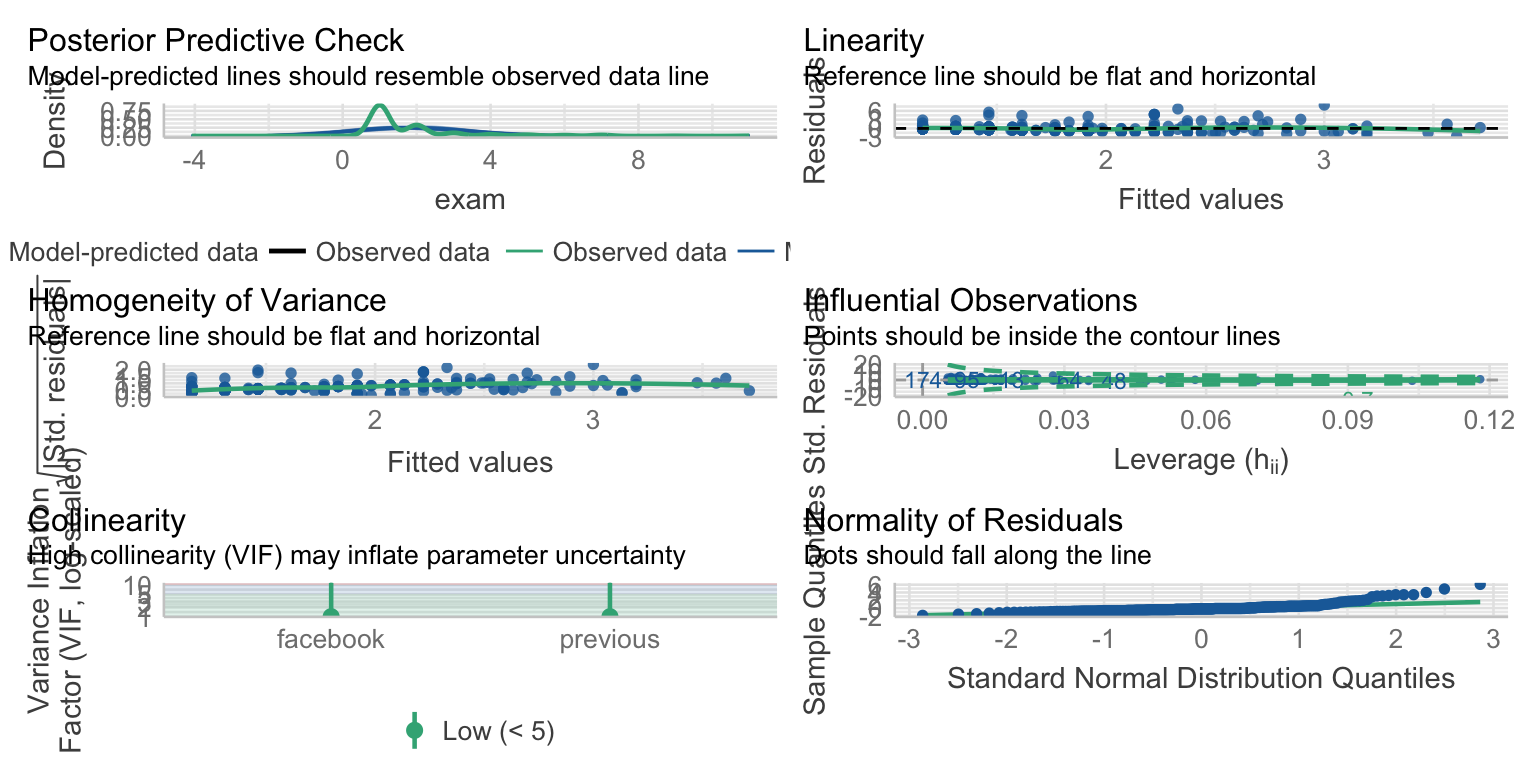
- X + M -> Y JSmediation results: Assumptions
JSmediation: Indirect effect
# Testing Indirect Effect with `JSmediation`
model_fit_with_index <- add_index(mediation_fit)
model_fit_with_indexTest of mediation (simple mediation)
==============================================
Variables:
- IV: facebook
- DV: exam
- M: previous
Paths:
==== ============== ===== =======================
Path Point estimate SE APA
==== ============== ===== =======================
a -0.211 0.097 t(237) = 2.17, p = .031
b 0.260 0.084 t(236) = 3.09, p = .002
c -0.661 0.128 t(237) = 5.16, p < .001
c' -0.606 0.127 t(236) = 4.77, p < .001
==== ============== ===== =======================
Indirect effect index:
- type: Indirect effect
- point estimate: -0.0547
- confidence interval:
- method: Monte Carlo (5000 iterations)
- level: 0.05
- CI: [-0.126; -0.00442]
Fitted models:
- X -> Y
- X -> M
- X + M -> Y Multiple Mediators
Test the influence of multiple mediator
Specific indirect effect
X -> M_1 -> Y
X -> M_2 -> Y
Total indirect effect
- Overall influence of mediators
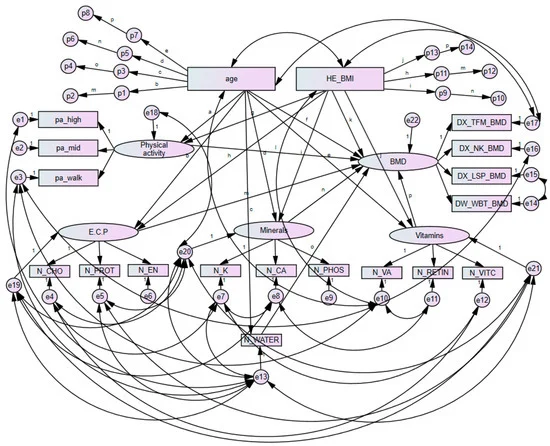
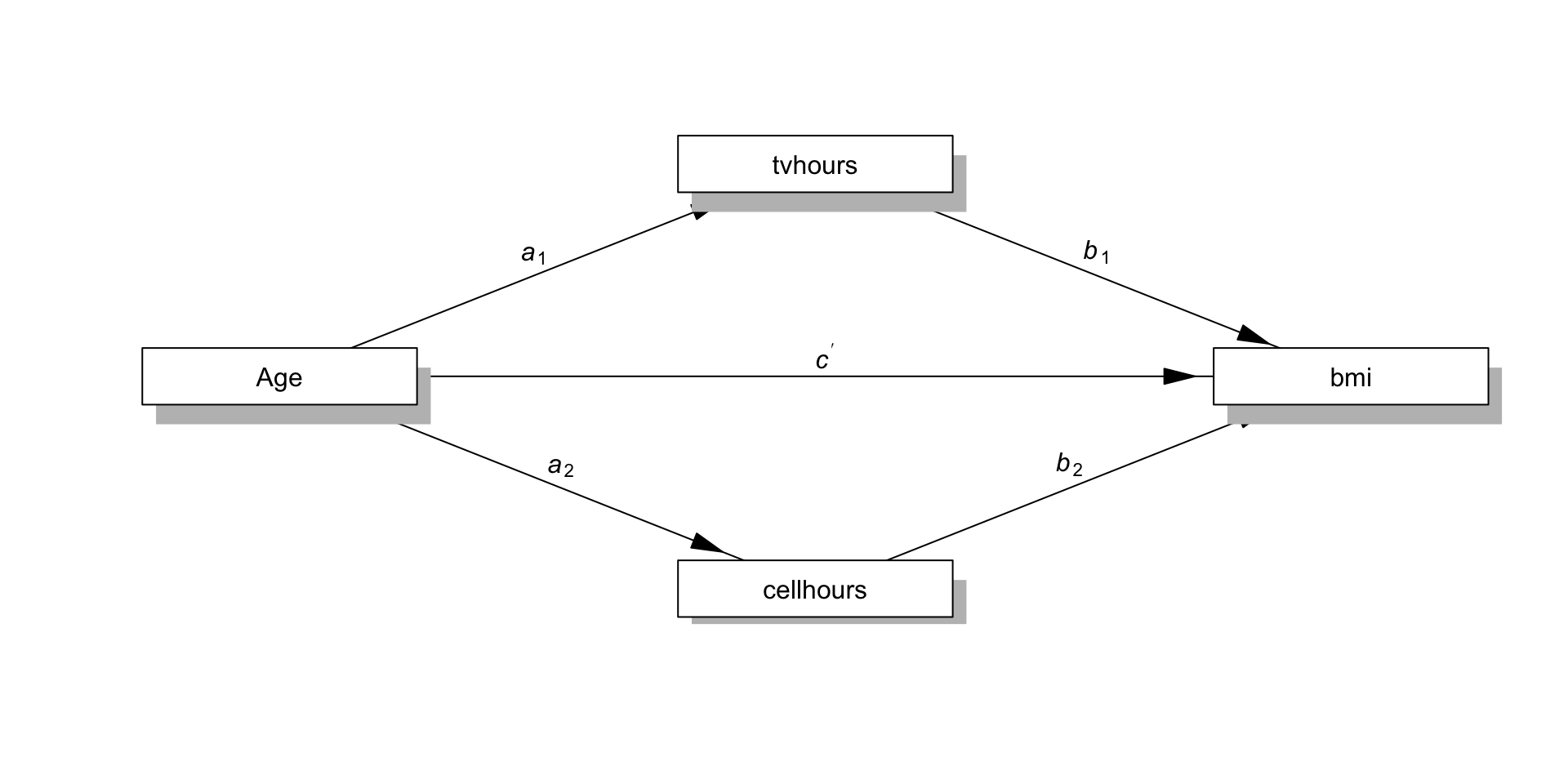
Multiple mediators: Example
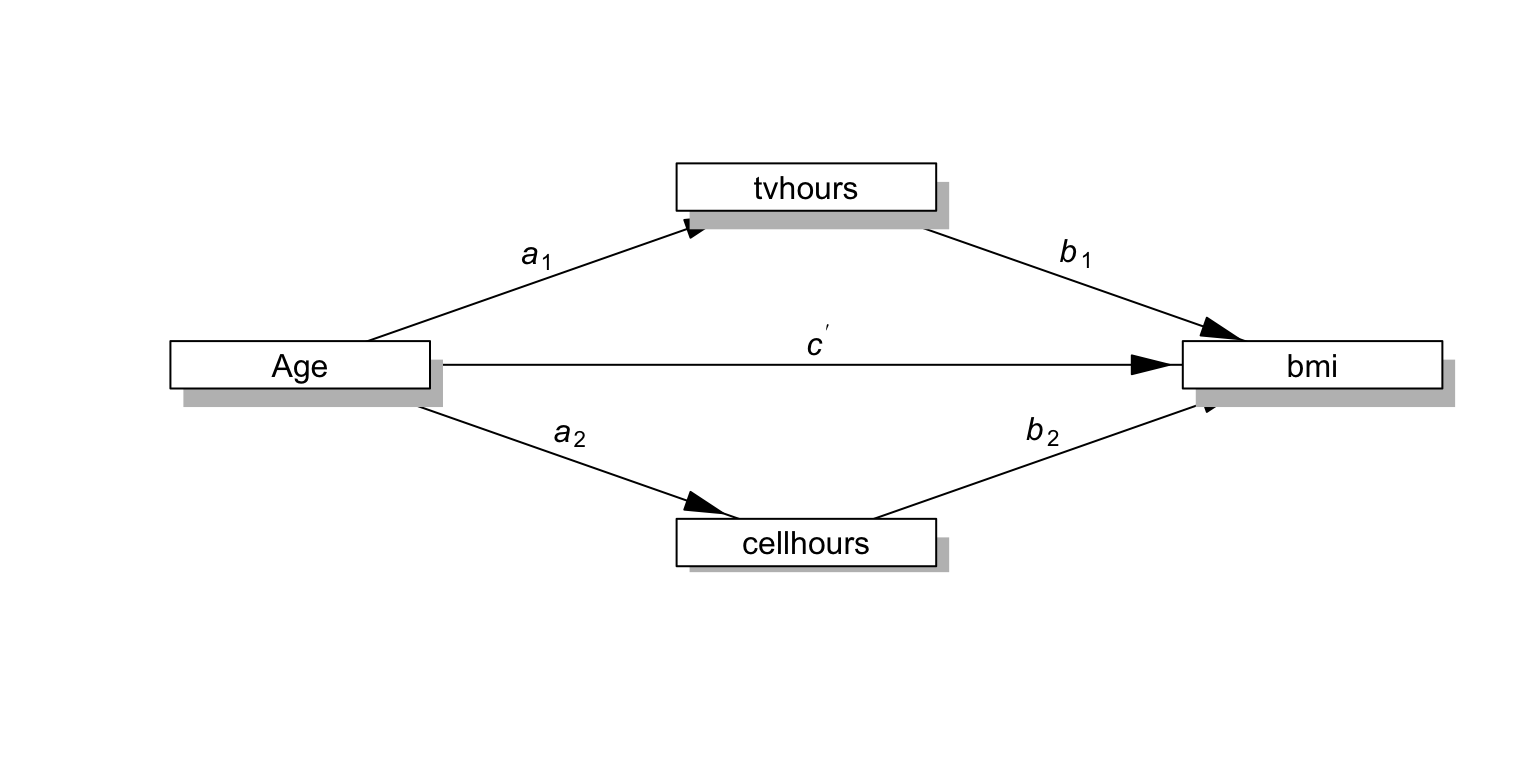
Lavaan
- Similar to MPlus, but free!
library(lavaan)
multipleMediation <- '
bmi ~ b1 * tvhours + b2 * cellhours + cp * age
tvhours ~ a1 * age
cellhours ~ a2 * age
# indirect 1
indirect1 := a1 * b1
# indirect 2
indirect2 := a2 * b2
# total
total := cp + (a1 * b1) + (a2 * b2)
total_indirect := (a1 * b1) + (a2 * b2)
#prob mediated
#prop_indirect1
prop_med_1 := indirect1 / (indirect1+cp)
prop_med_2 := indirect2 / (indirect2+cp)
prop_med := total_indirect /(total_indirect+cp)
#covariance
cellhours ~~ tvhours
'
fit <- sem(model = multipleMediation, data = weight_behavior, se = "bootstrap", bootstrap = 500)
# you should run 5000-10000 bootstrapsLavaan summary
lavaan 0.6.15 ended normally after 19 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 9
Number of observations 543
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Bootstrap
Number of requested bootstrap draws 500
Number of successful bootstrap draws 499
Regressions:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
bmi ~
tvhours (b1) 0.120 0.125 0.955 0.340 -0.119 0.367
cellhours (b2) 0.217 0.126 1.727 0.084 -0.030 0.461
age (cp) 0.026 0.134 0.191 0.848 -0.332 0.204
tvhours ~
age (a1) 0.017 0.041 0.420 0.674 -0.074 0.094
cellhours ~
age (a2) 0.041 0.068 0.599 0.549 -0.034 0.252
Covariances:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
.tvhours ~~
.cellhours 0.473 0.075 6.265 0.000 0.316 0.618
Variances:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
.bmi 15.273 1.535 9.952 0.000 12.353 18.371
.tvhours 1.883 0.073 25.776 0.000 1.737 2.017
.cellhours 1.512 0.092 16.436 0.000 1.313 1.690
Defined Parameters:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
indirect1 0.002 NA -0.014 0.016
indirect2 0.009 NA -0.008 0.069
total 0.037 NA -0.308 0.223
total_indirect 0.011 NA -0.010 0.071
prop_med_1 0.074 NA -0.661 0.595
prop_med_2 0.257 NA -1.712 2.036
prop_med 0.299 NA -2.017 2.142Lavaan Plot
Within-participant mediation
Mediation when X is a within-subject variable
Dohle and Siegrist (2014, Exp 1)
Interested in the effect of name complexity on buying drugs
- The specific hypothesis is that complex drug names are perceived as more hazardous, which makes someone less likely to buy the drug
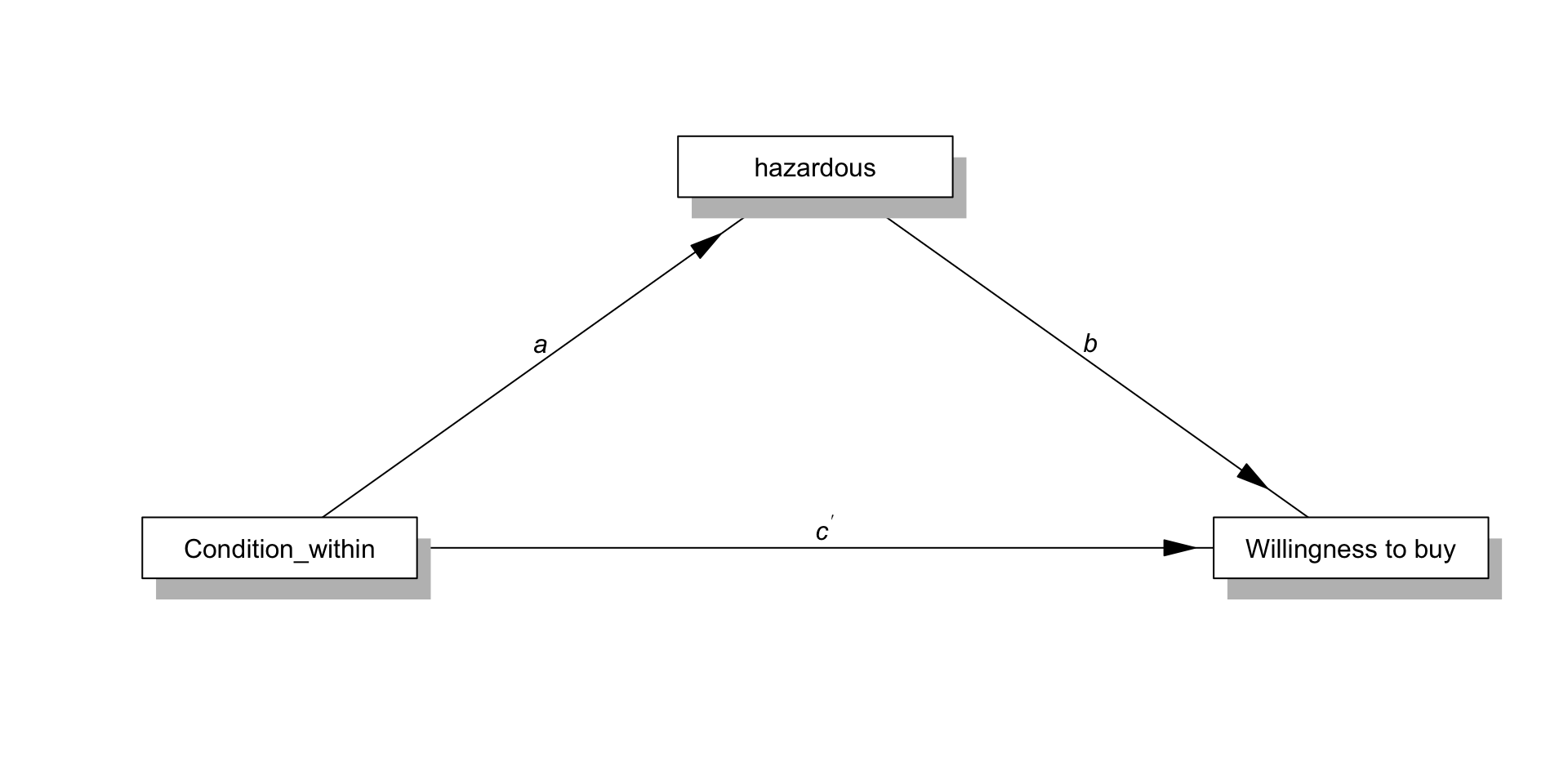
Within-participant mediation
\[ Y_{2i} - Y_{1i} = c_{11} \]
with Y2i−Y1i the difference score between DV conditions for the outcome variable for the ith observation
\[ M_{2i}-M_{1i} = a_{21} \]
with \(M_{2i}\)−$M1_{1i}$ the difference score between DV conditions for the mediator variable for the ith observation,
\[ Y_{2i} - Y_{1i} = c'_{31} + b_{32}(M_{2i}-M_{1i}) + d_{33}[0.5(M_{2i}+M_{1i}) - 0.5(\bar{M_1}+ M_2})] \] Where we have the mediator diff and mean_diff
Within-participant mediation
- Montoya, A. K., & Hayes, A. F. (2017). Two-condition within-participant statistical mediation analysis: A path-analytic framework. Psychological Methods, 22(1), 6-27. doi: 10.1037/met0000086
Within-participant indirect effect
Test of mediation (within-participant_mediation)
==============================================
Variables:
- IV: name (difference: simple - complex)
- DV: willingness
- M: hazardousness
Paths:
==== ============== ===== ======================
Path Point estimate SE APA
==== ============== ===== ======================
a -0.800 0.258 t(21) = 3.10, p = .005
b -0.598 0.113 t(19) = 5.29, p < .001
c 0.564 0.193 t(21) = 2.92, p = .008
c' 0.085 0.158 t(19) = 0.54, p = .596
==== ============== ===== ======================
Indirect effect index:
- type: Within-participant indirect effect
- point estimate: 0.479
- confidence interval:
- method: Monte Carlo (5000 iterations)
- level: 0.05
- CI: [0.158; 0.88]
Fitted models:
- 1 -> DV_diff
- 1 -> M_diff
- 1 + M_diff + M_mean -> DV_diff Summary: Mediation
What it is: A method for testing hypotheses about why x predicts y
When you use it:
Whenever you would start using words like “because” in your introduction section; it tests “how” and “why” questions
Whether there is a basic relationship between x and y or not
Best approach*:
- Bootstrapping
Write-up: Simple mediation
a, b paths
Direct effect (c’)
Total effect (c)
Indirect effect
Sobel/Arioan, Bootstrapping (# bootstrapped samples)
Figure of path diagram
- Create in PPT 😱
- Use DiagrammeR
Write up: Multiple mediators
Include all indirect effects
Total indirect effect
Proportion mediated
PSY 504: Advanced Statistics