Multilevel Modeing (with R)

Princeton University

Jason Geller, PH.D.

4/24/23

Overview

  • What are multilevel models and why are they awesome?

  • Important terminology

  • Interpretation, estimation, and visualization of multilevel models in R

  • Writing up MLM results

What we wont have time to talk about 😿

  • Cross-classified models

  • Partial-pooling/shrinkage

  • Growth curve modeling

  • Different types of degrees of freedom

  • Centering

  • Effective sample size

  • Power

  • Cross-level interactions

If you have specific questions about these things ask me

Why multilevel modeling?

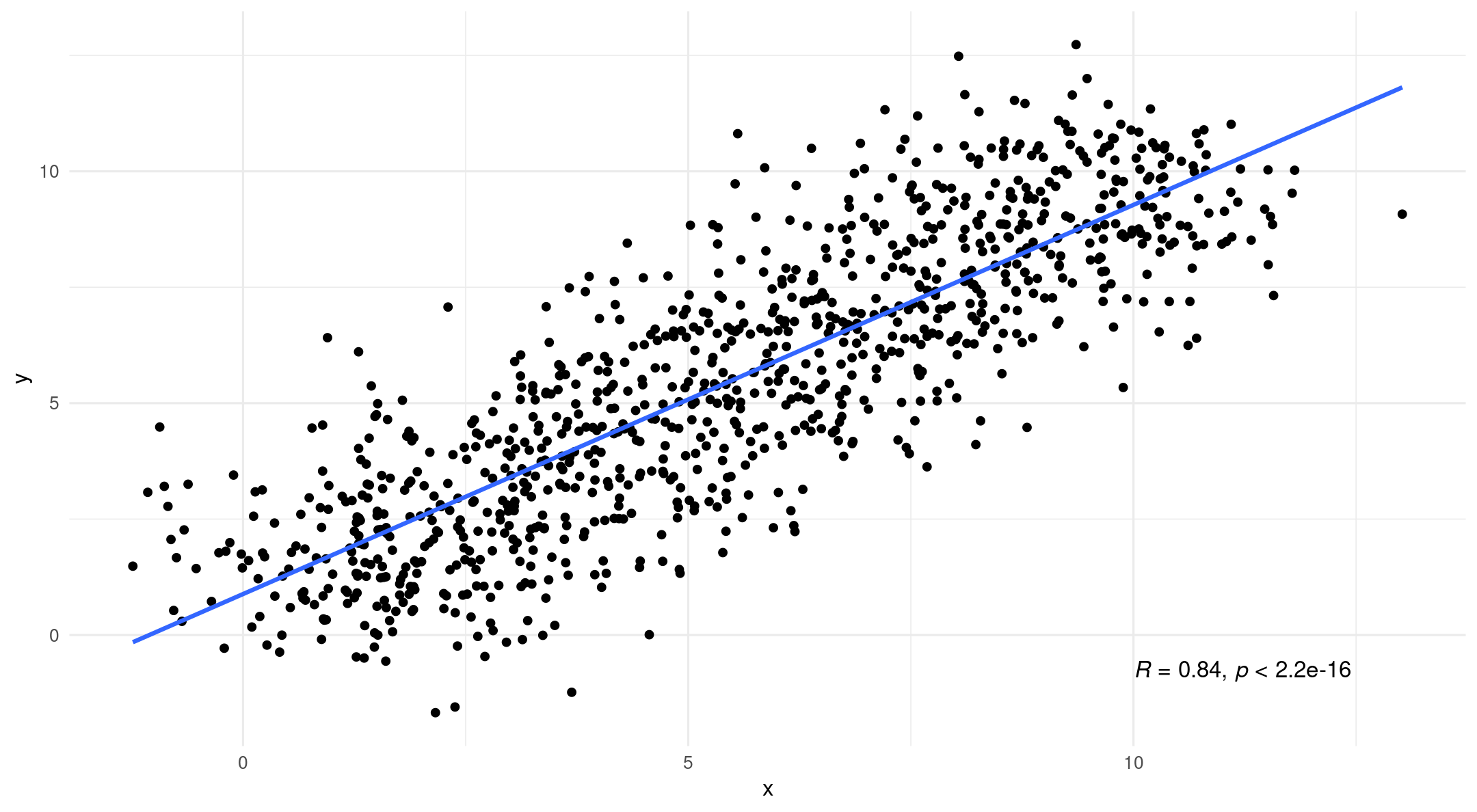
  • You might be used to your data looking like this: An independent variable (x) and a dependent variable (y)

Why multilevel modeling?

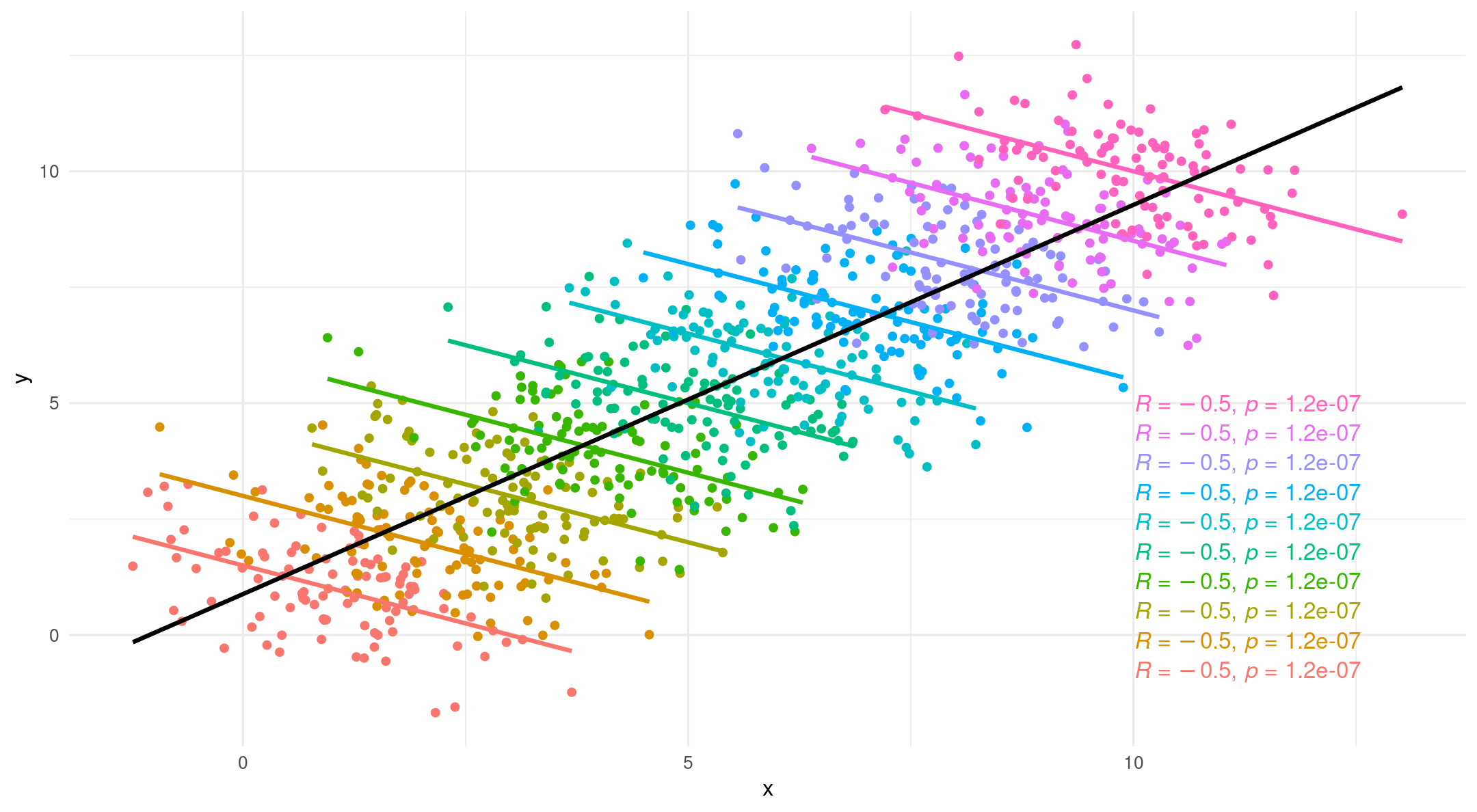
  • However, if we introduce grouping we tell a different story

What is multilevel modeling?

  • Simpson’s Paradox

What is multilevel modeling?

What is multilevel modeling?

  • An elaboration on regression to deal with non-independence between data points (i.e., clustered data)

Hierarchies

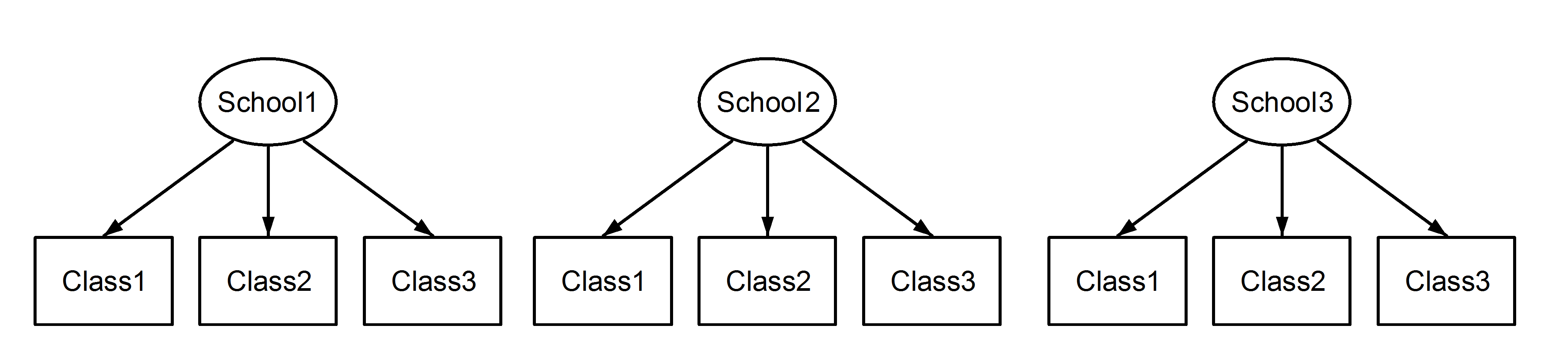
  • For now we will focus on data with two levels:
    • Level one: most basic level of observation
    • Level two: groups formed from aggregated level-one observation

Multilevel models are awesome!

  • Interdependence
    • You can model the relationships between cases (regression for repeated observations)
  • Missing data
    • Uses ML for missing data (partial pooling or shrinkage)
  • Power
    • Deaggregated data
  • Take into account within and between variance
  • Flexibility

Multilevel models

  • When to use them:

    • Nested designs

    • Repeated measures

    • Longitudinal data

  • Why use them:

    • Captures variance occurring between groups and within groups

  • What they are:

    • Linear model with extra residuals

Important Terminology

Jumping right in

  • Words you hear constantly in MLM Land:

    • Fixed effects
    • Random effects
    • Random intercepts
    • Random slopes

  • What do they all mean?

Today’s data

  • What did you say?

    • Ps (N = 31) listened to clear (NS) and 6 channel vocoded speech (V6)
      • (https://www.mrc-cbu.cam.ac.uk/personal/matt.davis/vocode/a1_6.wav)

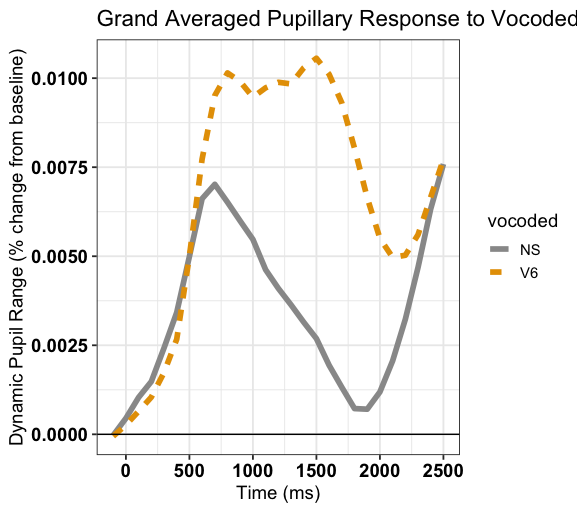
Data



library(tidyverse)
library(lme4) # fit mixed models
library(broom.mixed) # tidy output of mixed models
library(afex) # fit mixed models
library(emmeans) # marginal means
library(ggeffects) # marginal means
eye  <- read_csv("https://raw.githubusercontent.com/jgeller112/psy504-advanced-stats/main/slides/MLM/data/vocoded_pupil.csv")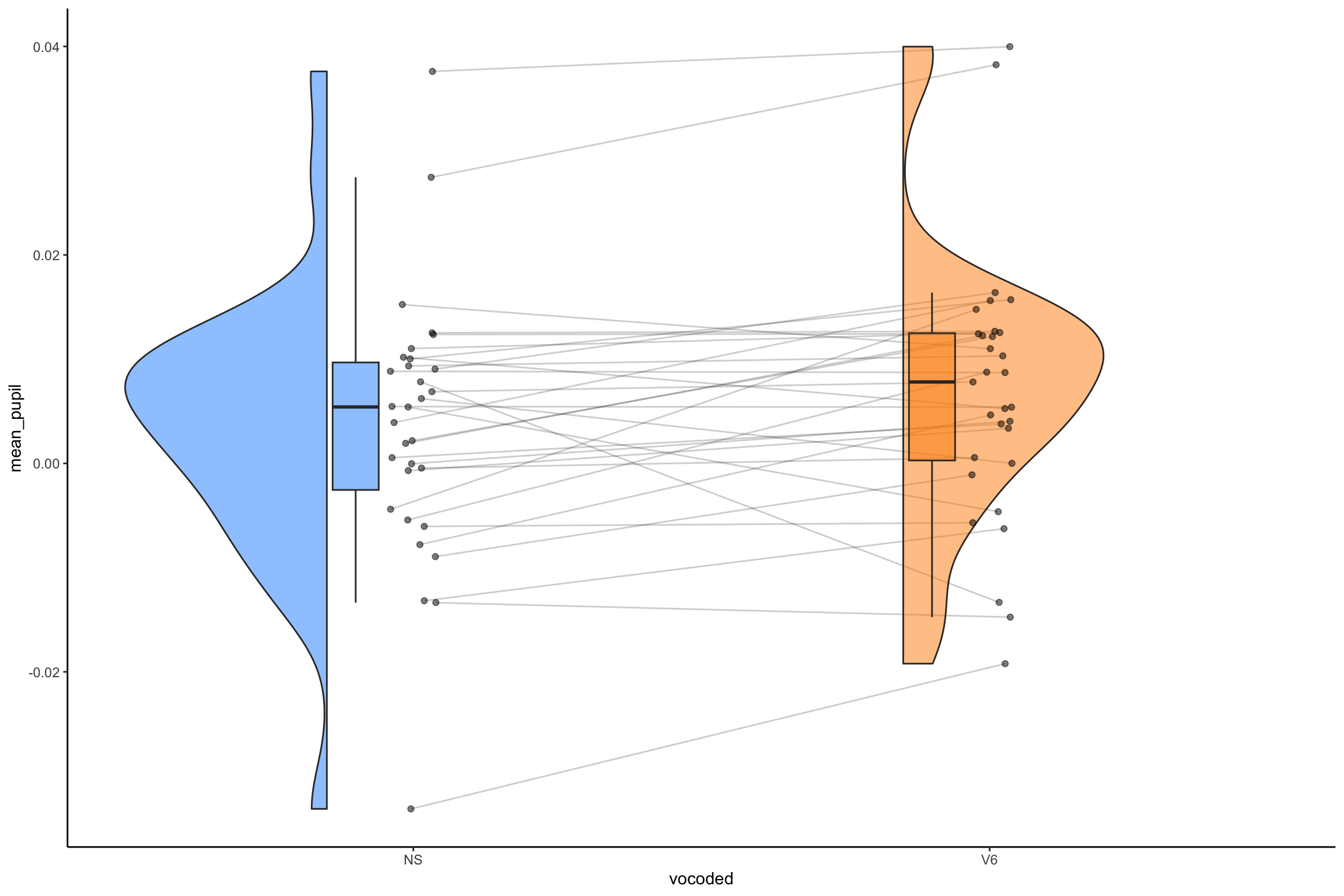

Fixed and random effects

  • Fixed effect:

    • Assumed to be constant

    • Population-level (i.e., average) effects that should persist across experiments

    • Usually experimental manipulations

    • Can be continuous or categorical

  • In our data: vocoded

Fixed and random effects

  • Random effects:

    • Assumed to vary at the group/cluster-level

      • Randomly sampled observations over which you plan to generalize

        • Participants
        • Schools
        • Words
        • Pictures

  • Can help account for individual variation

  • In our data: subject

Random intercepts

  • Varying starting point (intercept), same slope for each group

    • (1|participant): random intercept for group

      lmer(DV ~ (1|participant))

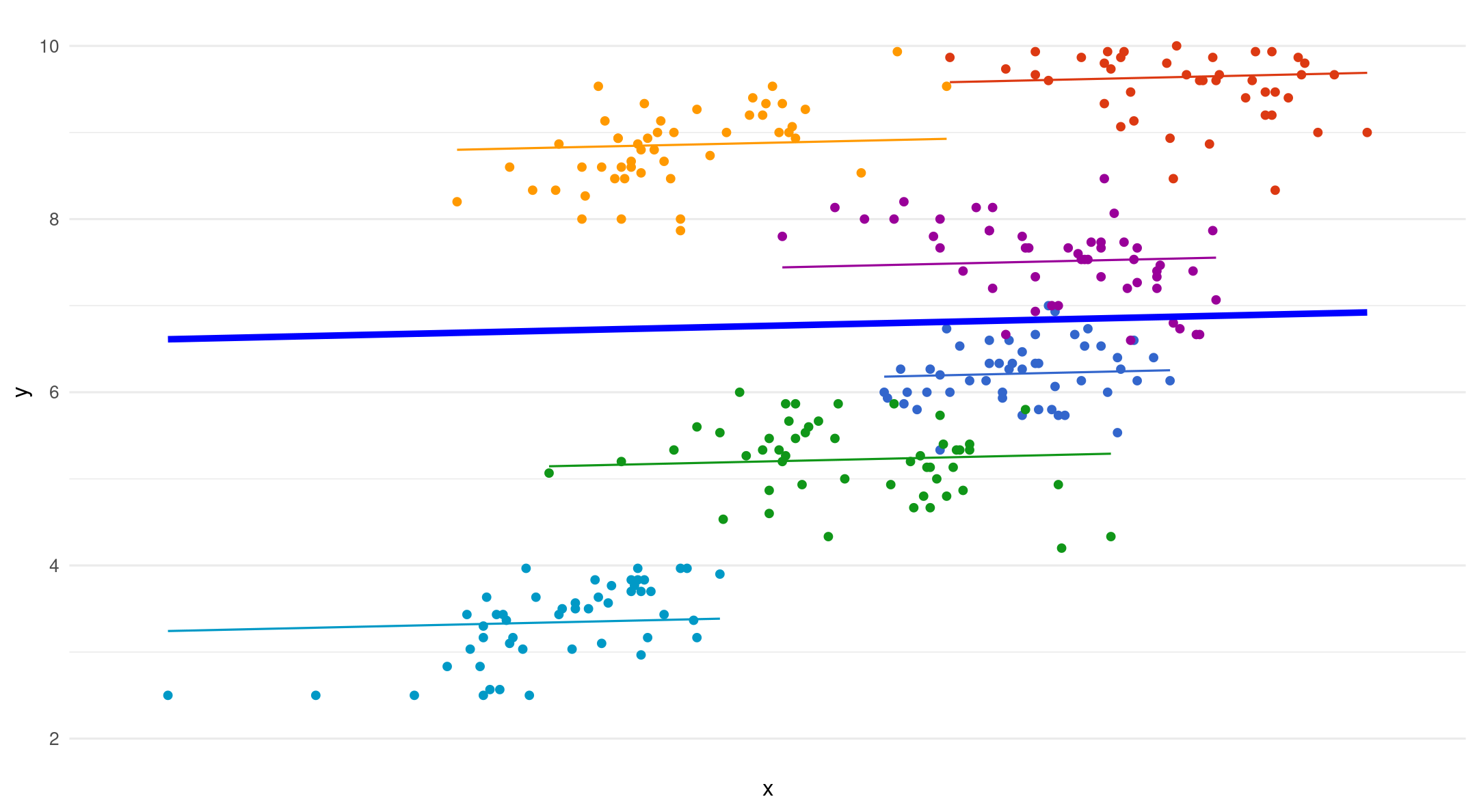
Random intercepts

  • In a multilevel model, error terms for individual data points are estimated by group

    • Person-specific deviation from group’s predicted outcome

      \[ y_{ij} = (\beta_{0} + u_{0j}) \]

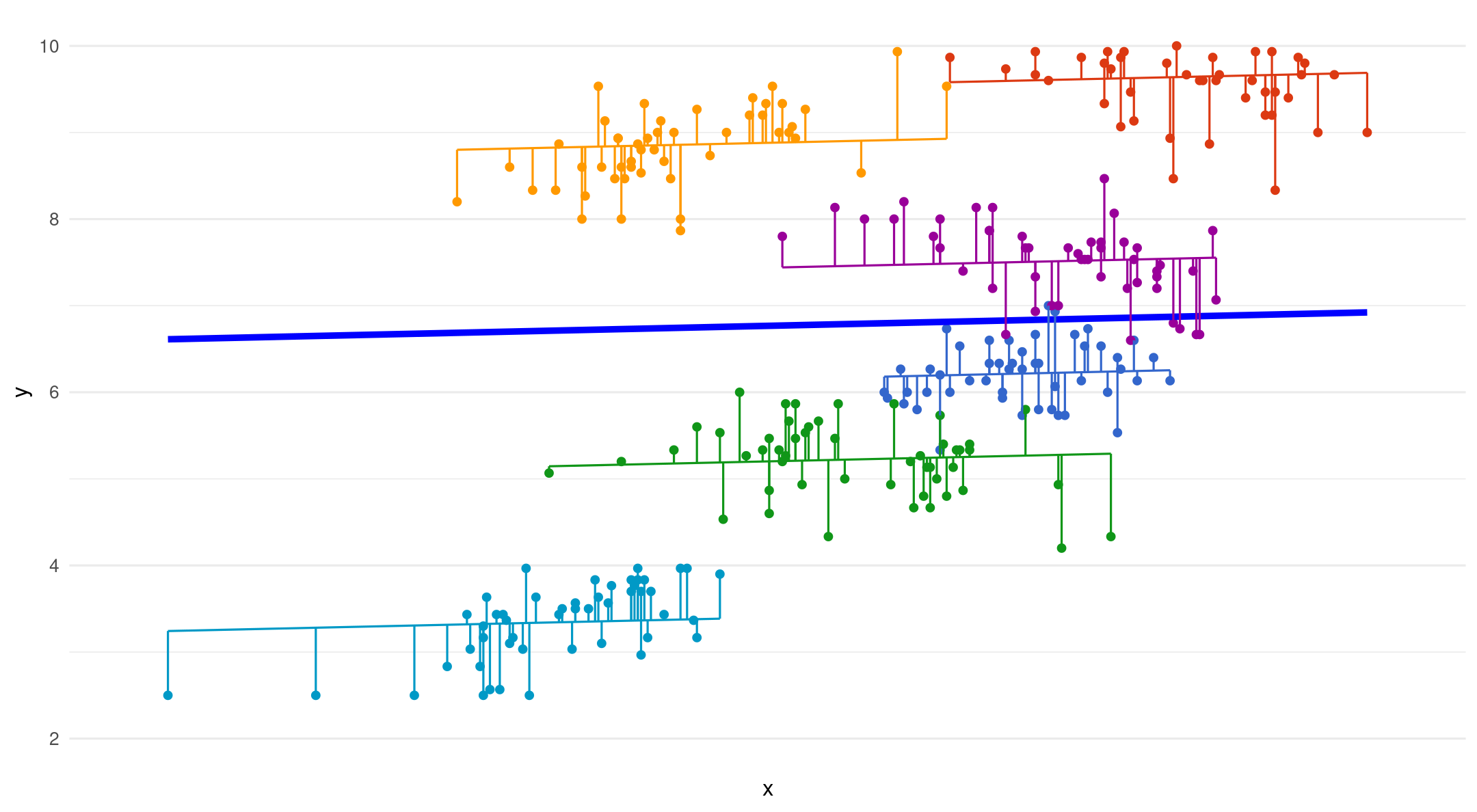
Random intercepts - fixed slopes

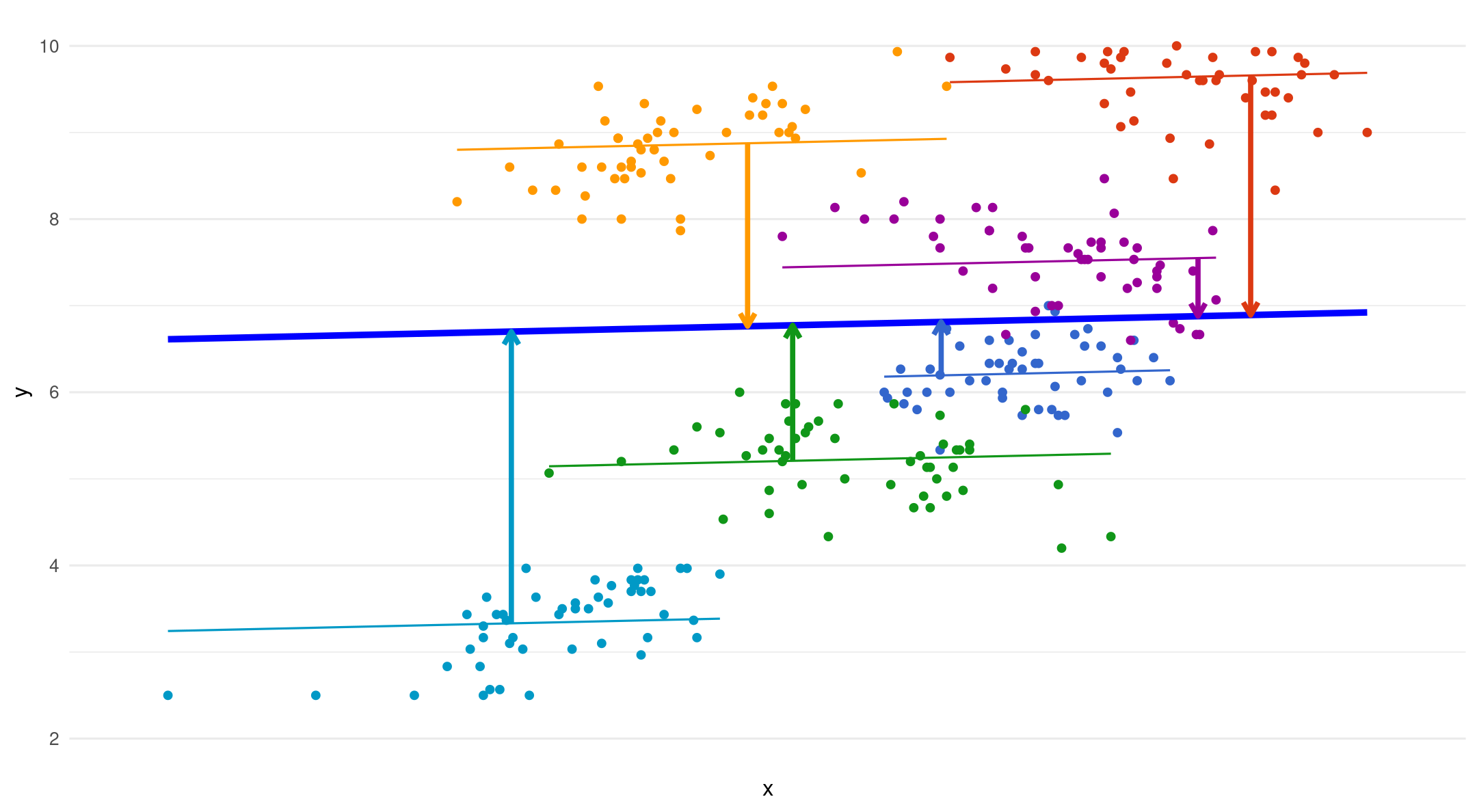
Random intercepts - random slopes

  • Varying starting point (intercept) and slope per group

    • (1+vocoded|group): random intercept and slopes per group

      • Only put a random slope if it changes within cluster/group

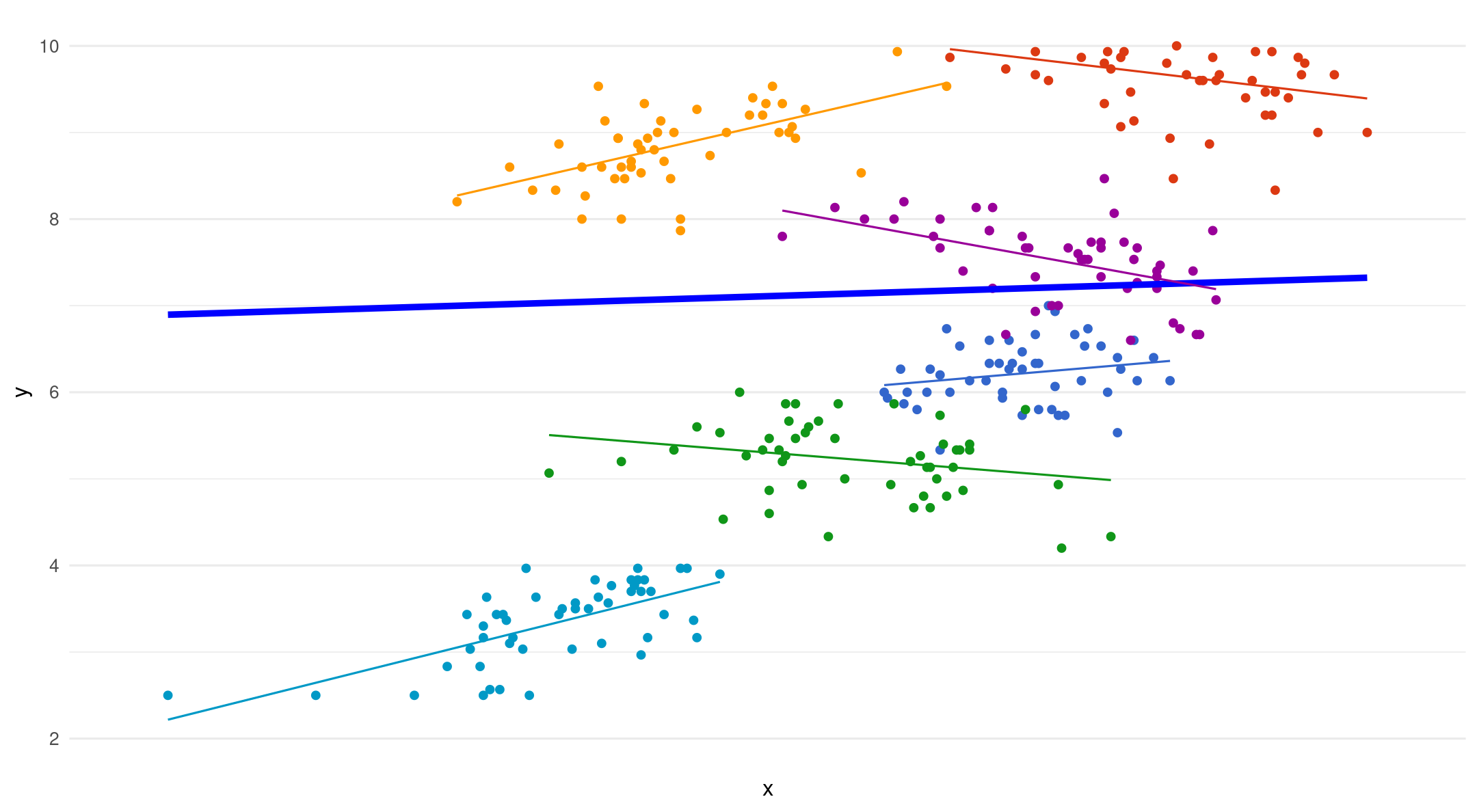
        lmer(DV ~ vocoded + (1+vocoded|participant))

Random intercepts - random slope

  • The dotted lines are fixed slopes. The arrows show the added error term for each random slope

\[ y_{ij}=(\beta_{1} + u_{1j}) \]

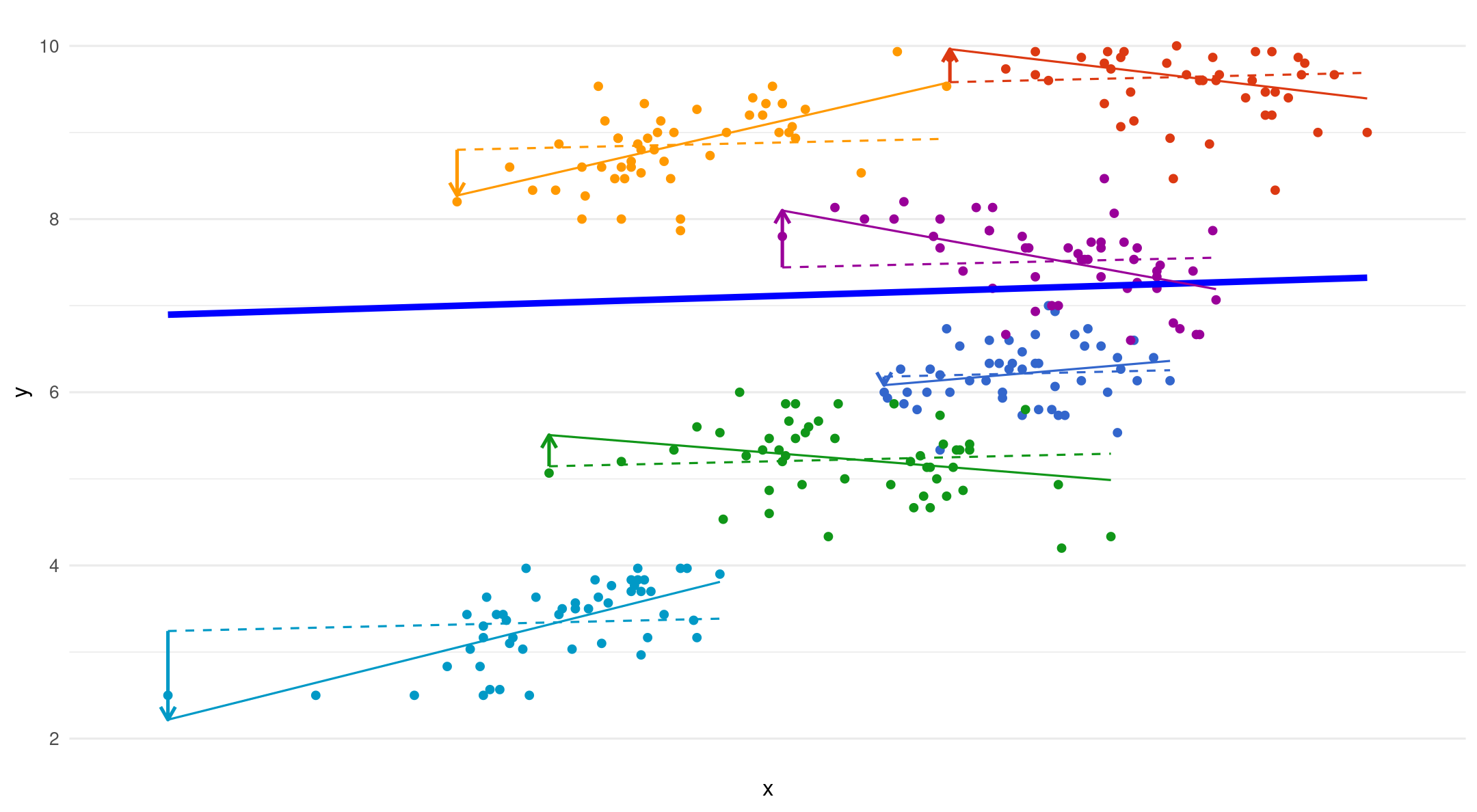
All together

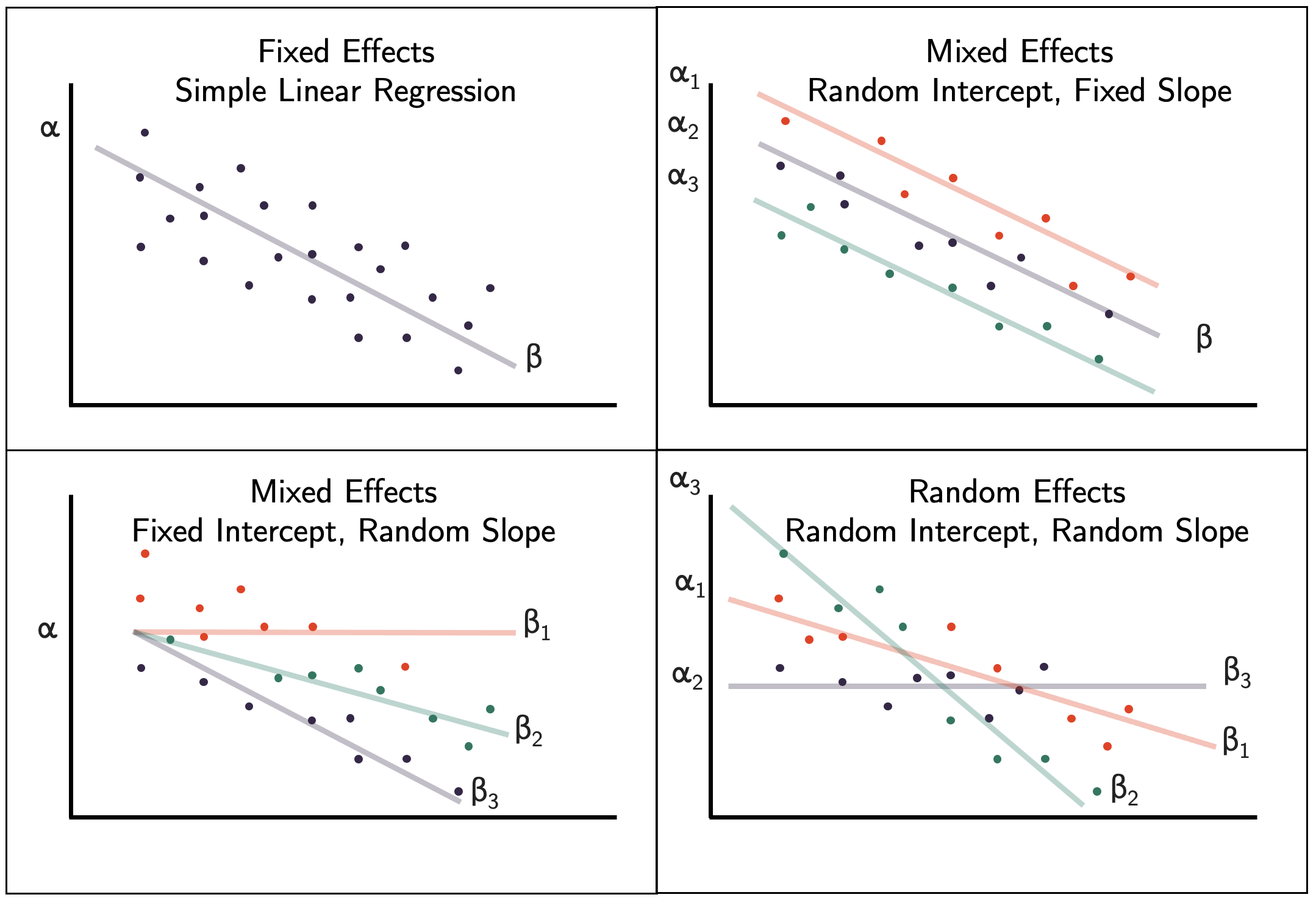
Combined multilevel equation

  • Level 1: \[y_{ij} = \beta_{0j} + \beta_{1j}x_{ij} + e_{ij}\]
  • Level 2:

\[ Random Intercept = \beta_{0j} = \beta_{0} + u_{0j}\]

\[Random{slope}=\beta_{1j} = \beta_{1} + u_{1j}\]

  • Mixed Model Equation

\[y_{ij} = (\beta_{0} + u_{0j}) + (\beta_{1} + u_{1j})x_{ij} + e_{ij}\]

Modeling

Data organization

  • Data Structure

    • MLM analysis requires data in long format
...1subjecttrialvocodedmean_pupil
1EYE153V60.084   
2EYE154V60.0141  
3EYE155V60.0225  
4EYE156V60.000742
5EYE157V60.0243  
6EYE158V60.0268  

Model selection

  • Forward or backward approach

    • Model 1: Null (unconditional means) model (calculate ICC)

    • Model 2: full (maximal) model

      • if non-convergence (pay attention to warning messages):

        • Try different optimizers 1

        • Deal with random effects

    • Model 3 (optional): remove fixed effects (e.g., interaction)

Model fitting: ML or REML

  • Two flavors of maximum likelihood

    • Maximum Likelihood (ML or FIML)

      • Jointly estimate the fixed effects and variance components using all the sample data

      • Can be used to draw conclusions about fixed and random effects

      • Issue: Fixed effects are treated as known values when estimating variance components

        • Results in biased estimates of variance components (especially when sample size is small)

Model fitting: ML or REML

  • Restricted Maximum Likelihood (REML)

    • Estimate the variance components using the sample residuals not the sample data

    • It is conditional on the fixed effects, so it accounts for uncertainty in fixed effects estimates

      • This results in unbiased estimates of variance components

Model fitting: ML or REML?

  • Research has not determined one method absolutely superior to the other

  • REML (REML = TRUE; default in lmer) is preferable when:

    • The number of parameters is large or primary, or

    • Primary objective is to obtain estimates of the model parameters

  • ML (REML = FALSE) must be used if you want to compare nested fixed effects models using a likelihood ratio test (e.g., a drop-in-deviance test)

  • For REML, the goodness-of-fit and likelihood ratio tests can only be used to draw conclusions about variance components

Check assumptions

  • Linearity

  • Normality

  • Homoscedasticity

  • Collinearity

  • Outliers

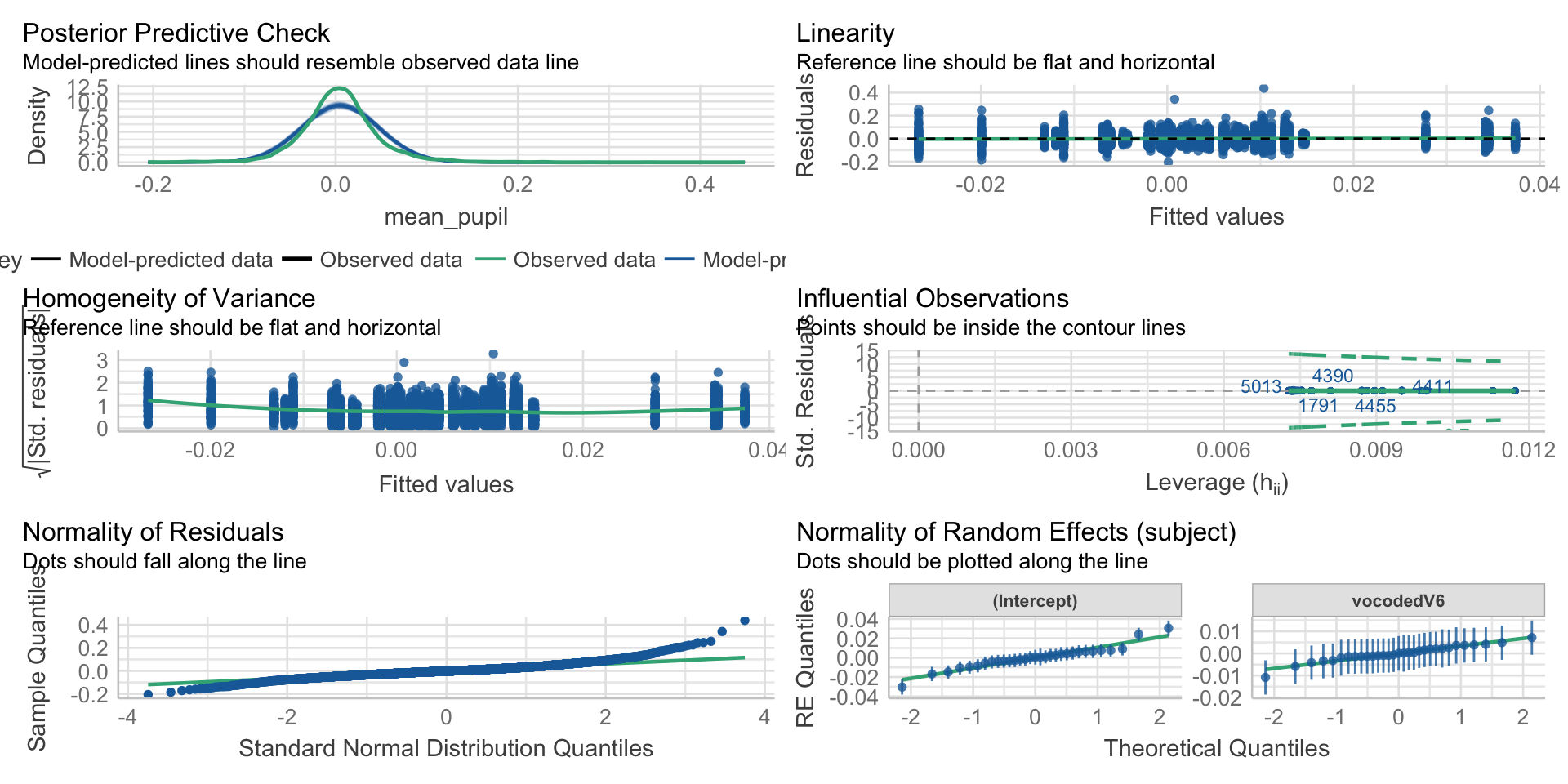
Fitting and Interpreting Models

Linear regression

eye_agg <- eye %>%
  group_by(subject, vocoded)%>%
  summarize(mean_pupil=mean(mean_pupil))

lm_model <- lm(mean_pupil ~ vocoded, data = eye_agg)

tidy(lm_model)
termestimatestd.errorstatisticp.value
(Intercept)0.003570.002271.570.121
vocodedV60.003260.003211.010.315

Null model (unconditional means)

library(lme4) # pop linear modeling package

null_model <- lmer(mean_pupil ~ (1|subject), data = eye)

summary(null_model)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: mean_pupil ~ (1 | subject)
   Data: eye

REML criterion at convergence: -19811.6

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-5.1411 -0.5530 -0.0463  0.4822 10.8130 

Random effects:
 Groups   Name        Variance  Std.Dev.
 subject  (Intercept) 0.0001303 0.01142 
 Residual             0.0016840 0.04104 
Number of obs: 5609, groups:  subject, 31

Fixed effects:
             Estimate Std. Error        df t value Pr(>|t|)  
(Intercept)  0.005227   0.002124 29.457784   2.461   0.0199 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Intraclass correlation (ICC)

  • ICC is a standardized way of expressing how much variance is due to clustering/group

    • Ranges from 0-1

  • Also, can be interpreted as correlation among observations within cluster/group

  • If ICC is sufficiently low (i.e., \(\rho\) < .1), then you don’t have to use MLM! BUT YOU PROBABLY SHOULD 🙂

Calculating ICC

  • Run baseline (null) model

  • Get intercept variance and residual variance

\[\mathrm{ICC}=\frac{\text { between-group variability }}{\text { between-group variability+within-group variability}}\]

\[ ICC=\frac{\operatorname{Var}\left(u_{0 j}\right)}{\operatorname{Var}\left(u_{0 j}\right)+\operatorname{Var}\left(r_{i j}\right)}=\frac{\tau_{00}}{\tau_{00}+\sigma^{2}} \]

icc <- model_performance(null_model)

icc$ICC
[1] 0.07183568

Fixed effects

  • Interpretation same as lm
# add the fixed effect of vocode
inter_model <- lmer(mean_pupil ~vocoded+(1|subject), data = eye)

#grab the fixed effects
broom.mixed::tidy(inter_model) %>% filter(effect == "fixed")
effectgrouptermestimatestd.errorstatisticdfp.value
fixed(Intercept)0.003690.00221.6833.6     0.102  
fixedvocodedV60.003060.00112.795.58e+030.00526

  • Default behavior is leave out *p*-values (Doug Bates doesn’t like them)

    • Install `lmerTest` to include *p*-values

Random effects/variance components

  • Tells us how much variability there is around the fixed intercept/slope

    • How much does the average pupil size change between participants

      tidy(inter_model) %>% filter(effect == "ran_pars")
      effectgrouptermestimatestd.errorstatisticdfp.value
      ran_parssubjectsd__(Intercept)0.0114
      ran_parsResidualsd__Observation0.041 

Visualize random effects

#use easystats to grab group variance
random <- estimate_grouplevel(inter_model)

plot(random) +
  theme_lucid()

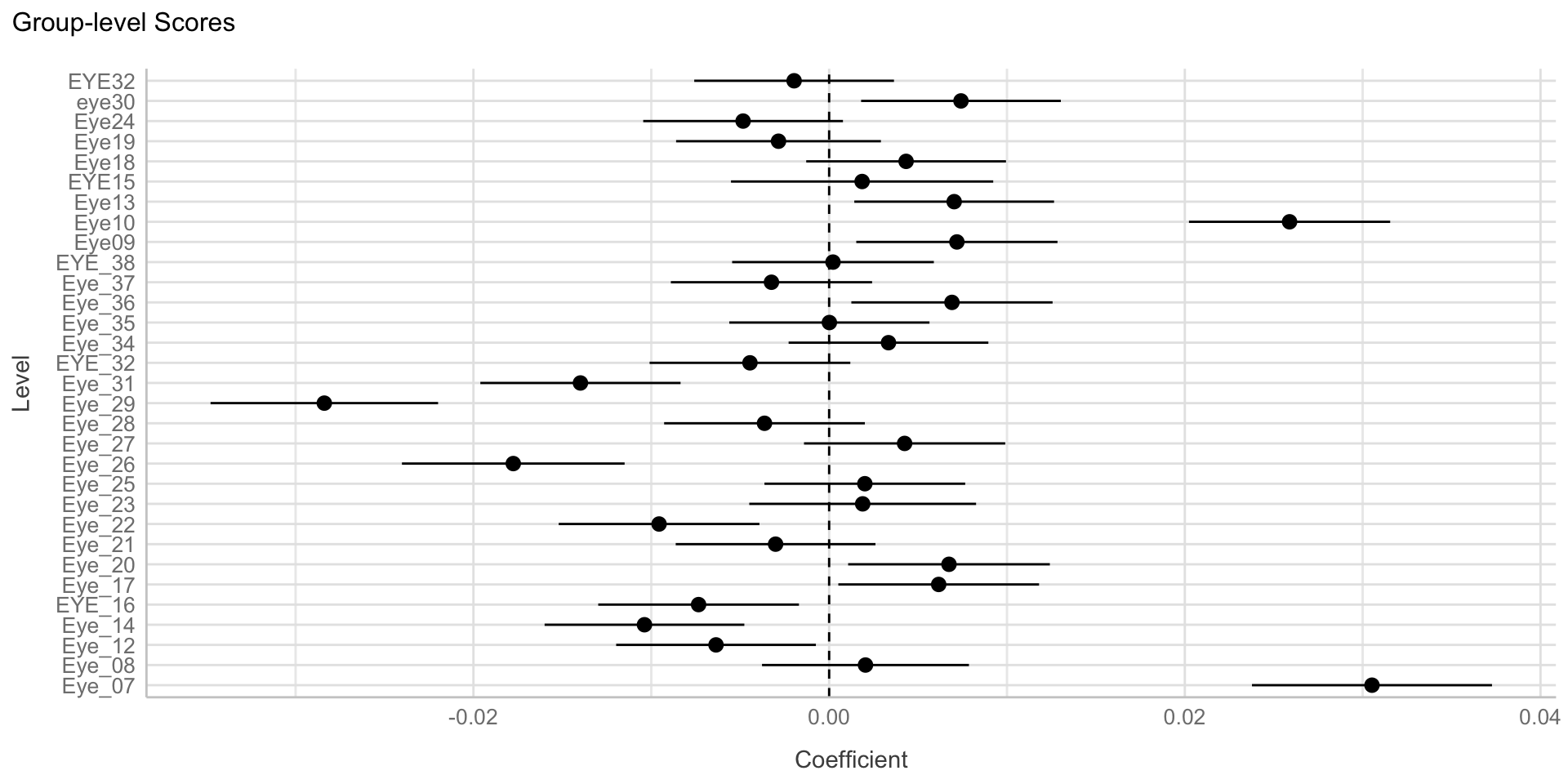
Maximal model: Fixed effect random intercepts (subject) and slopes (vocoded) model

max_model <- lmer(mean_pupil ~vocoded +(1+vocoded|subject), data = eye)

tidy(max_model)
effectgrouptermestimatestd.errorstatisticdfp.value
fixed(Intercept)0.003640.002231.6328.90.114 
fixedvocodedV60.003120.001452.1530.50.0396
ran_parssubjectsd__(Intercept)0.0117                 
ran_parssubjectcor__(Intercept).vocodedV6-0.195                  
ran_parssubjectsd__vocodedV60.00531                
ran_parsResidualsd__Observation0.0409                 

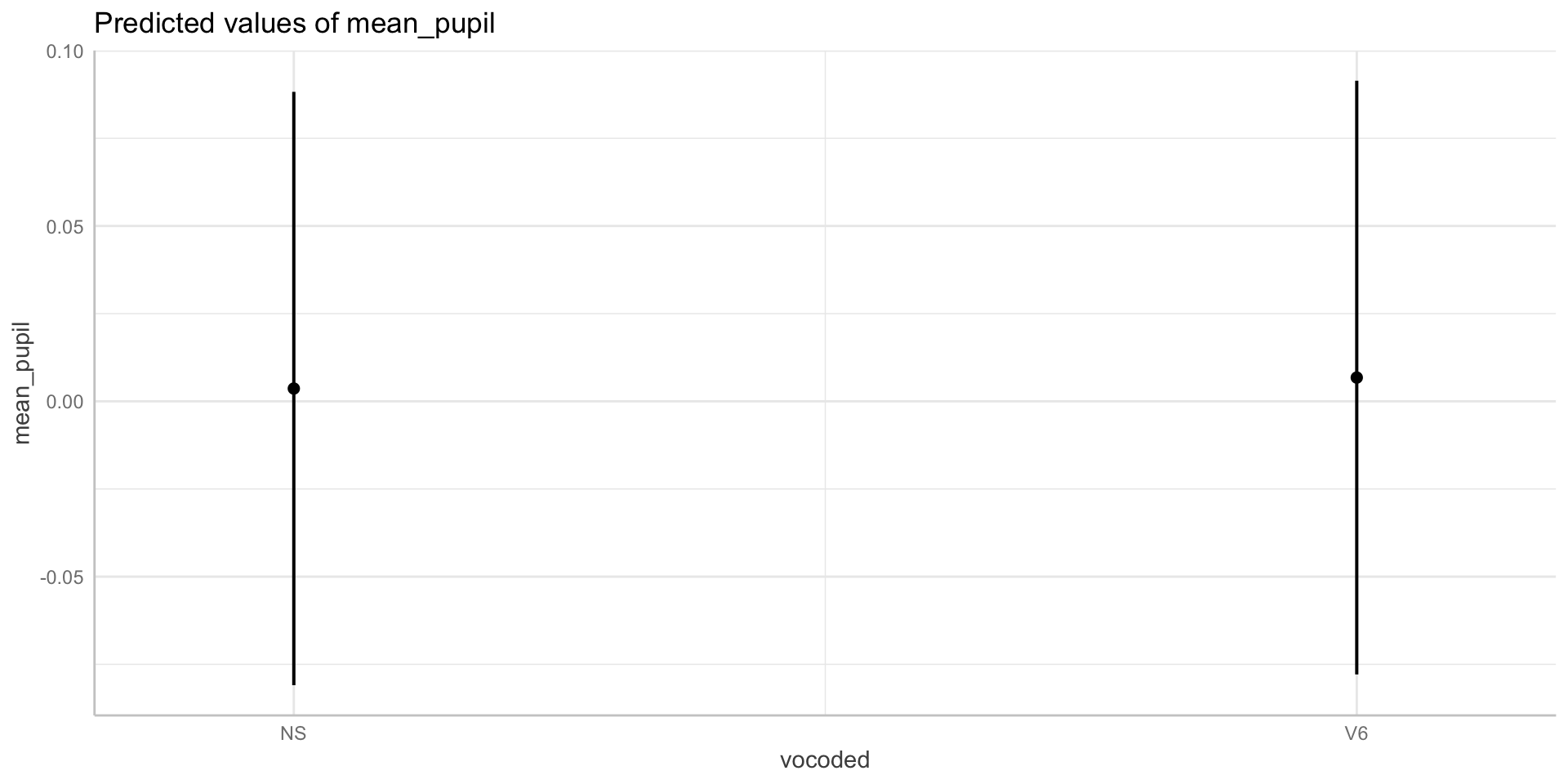
Using emmeans

  • Get factor means and contrasts
library(emmeans)

emmeans(max_model, specs = "vocoded") # grabs means for each level of modality
 vocoded  emmean      SE  df asymp.LCL asymp.UCL
 NS      0.00364 0.00223 Inf -0.000737   0.00802
 V6      0.00677 0.00226 Inf  0.002334   0.01120

Degrees-of-freedom method: asymptotic 
Confidence level used: 0.95 
emmeans(max_model, specs = "vocoded") %>%
  pairs() # use this to get pariwise compairsons between levels of factors
 contrast estimate      SE  df z.ratio p.value
 NS - V6  -0.00312 0.00145 Inf  -2.150  0.0316

Degrees-of-freedom method: asymptotic

Maximal models

  • Keep it maximal1

    • Whatever can vary, should vary

      • include random slopes only if it is a within cluster manipulation

    • Only when there is convergence issues should you remove terms

  • Decreases Type 1 error

Visualize random intercepts + slopes

random <- estimate_grouplevel(rand_model)

plot(random) +
  theme_lucid()

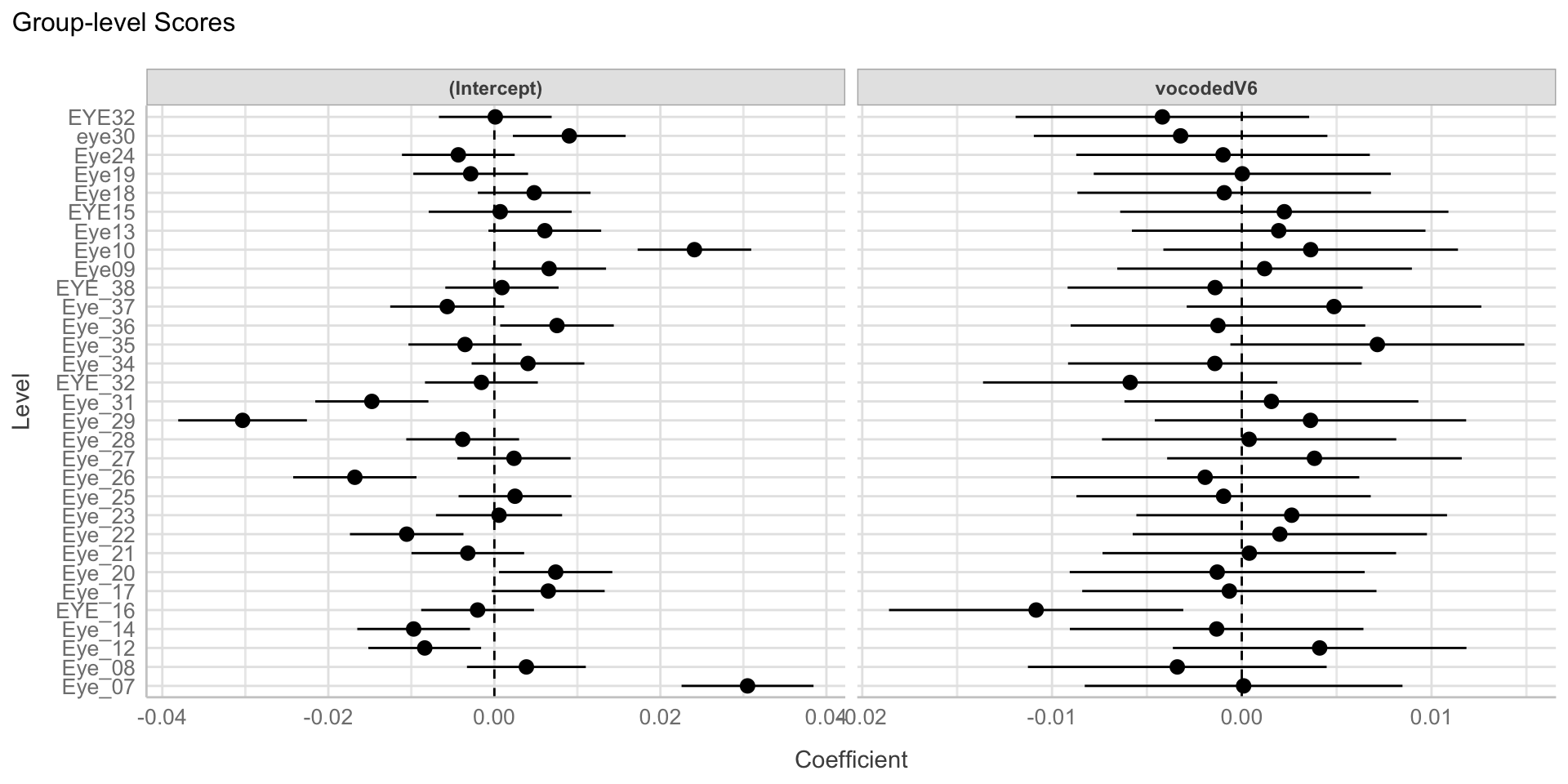
Random effects/variance components

  • Correlation between random intercepts and slopes

    • Negative correlation

      • Higher intercept (for normal speech) less of effect (lower slope)

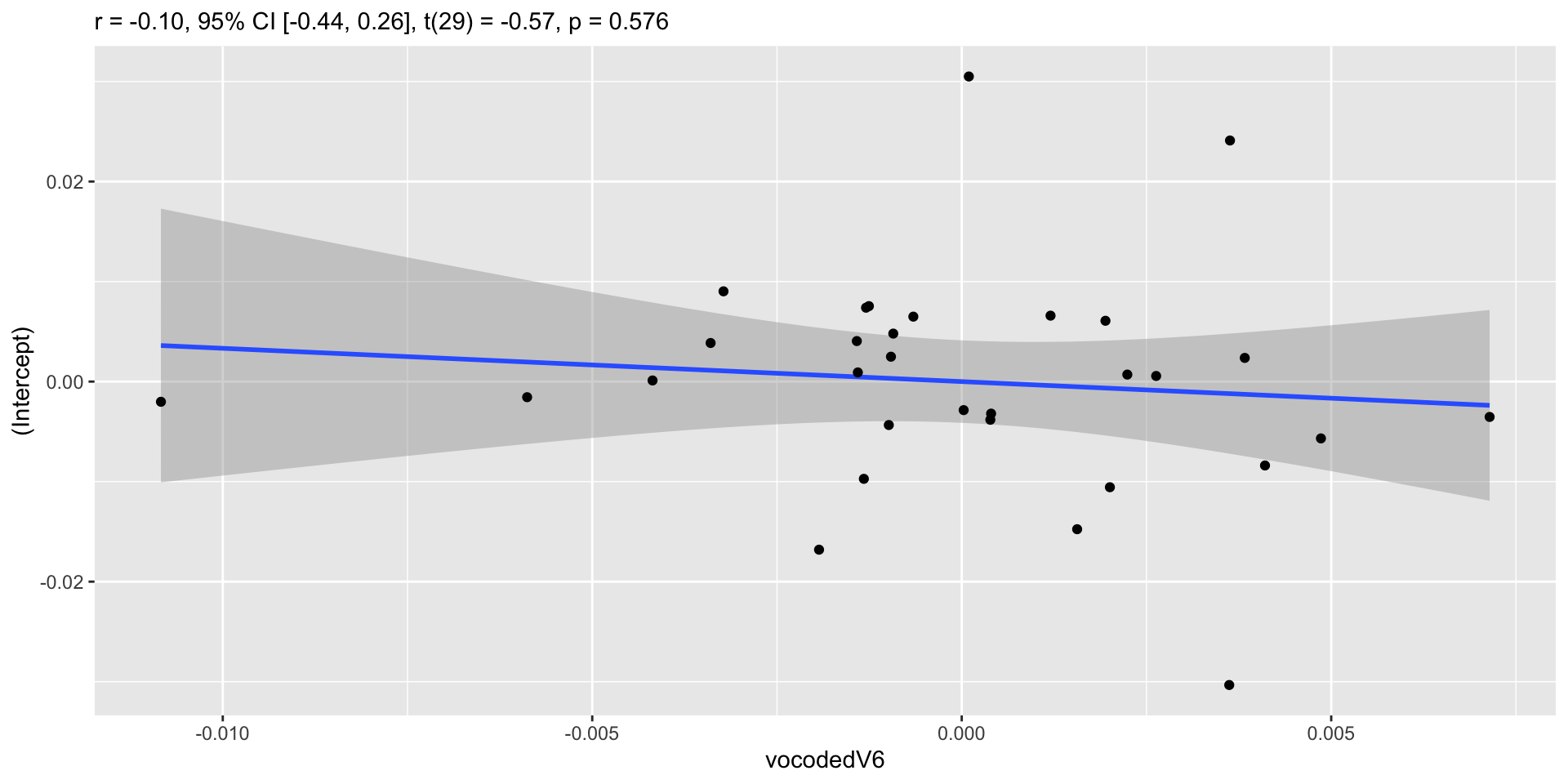
Model comparison

  • Can compare models using anova function or test_likelihoodratio from easystats

    • Will be refit using ML
#anova(null_model, inter_model, max_model)
test_likelihoodratio(null_model, inter_model, max_model)
NameModeldfdf_diffChi2p
null_modellmerModLmerTest3         
inter_modellmerModLmerTest417.790.00526
max_modellmerModLmerTest625.460.0651 

LRT

  • For more complex models, use LRT chi-square (drop-in deviance test)

    • Can be interpreted as main effects and interactions
    • Use afex
library(afex)

m <- mixed(mean_pupil ~ 1 + vocoded +  (1+vocoded|subject), data =eye, method = "LRT")

nice(m)
EffectdfChisqp.value
vocoded14.47 *.034

Visualization

Easystats

  • Easily visualize data
pupil_data_mean <- eye %>%
  group_by(subject, vocoded) %>%
  summarise(mean_pup=mean(mean_pupil, na.rm=TRUE)) %>% 
  ungroup()

mod_plot <- max_model %>%
  estimate_means("vocoded") %>%
  as.data.frame()

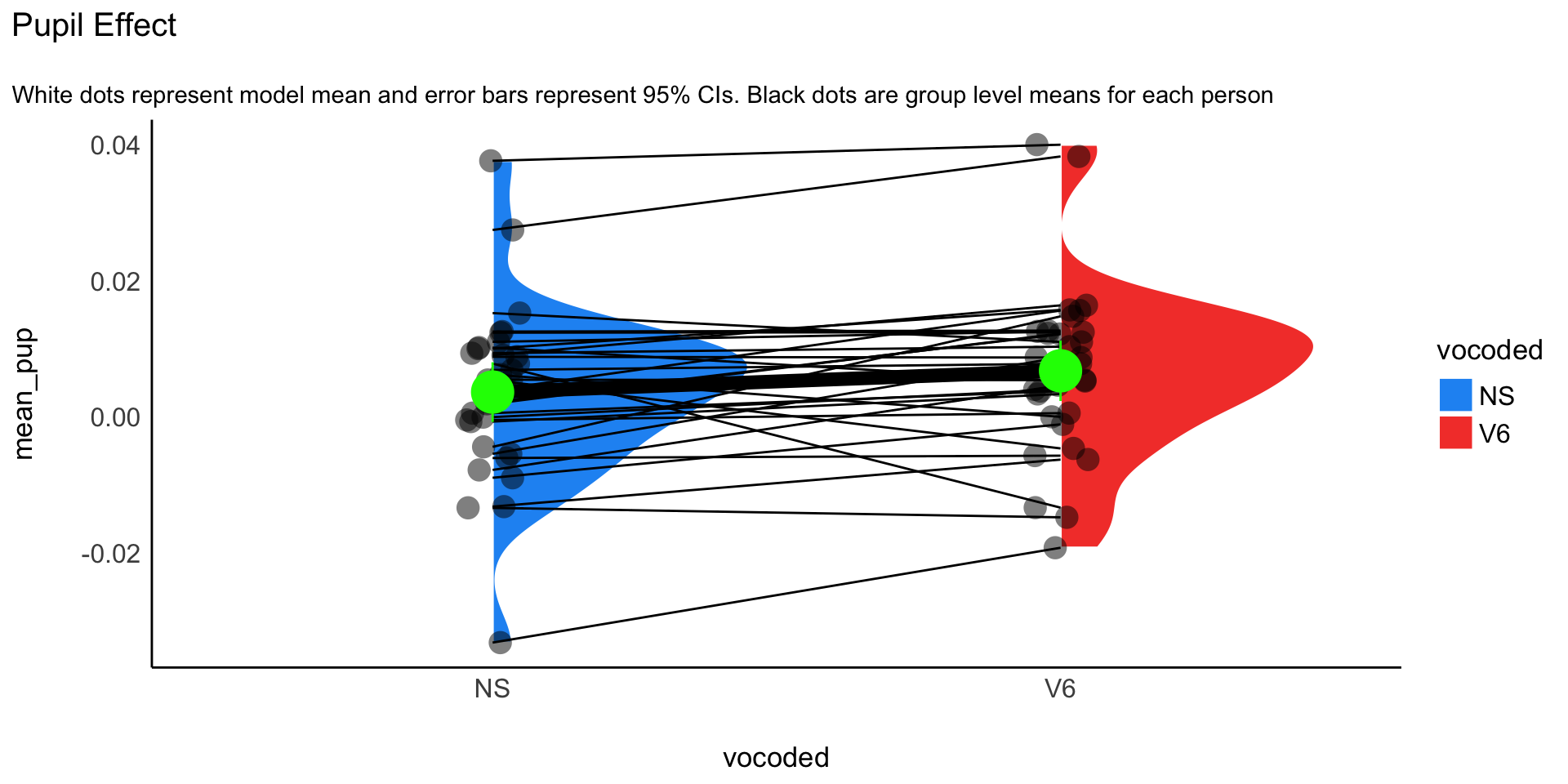
pupil_plot_lmer <- ggplot(pupil_data_mean, aes(x = vocoded, y = mean_pup)) +     
  geom_violinhalf(aes(fill = vocoded), color = "white") +
  geom_jitter2(width = 0.05, alpha = 0.5, size=5) +  # Add pointrange and line from means
  geom_line(aes(y=mean_pup, group=subject))+
  geom_line(data = mod_plot, aes(y = Mean, group = 1), size = 3) +
  geom_pointrange(
    data = mod_plot,
    aes(y = Mean, ymin = CI_low, ymax = CI_high),
    size = 2,
    color = "green"
  ) + 
  # Improve colors
  scale_fill_material() +
  theme_modern() + 
  ggtitle("Pupil Effect", subtitle = "White dots represent model mean and error bars represent 95% CIs. Black dots are group level means for each person")

Easystats

pupil_plot_lmer

ggeffects

ggemmeans(max_model, terms=c("vocoded"), type="re")%>% plot()

Effect size

  • Highly debated

    • Report pseudo-\(R^2\) for marginal (fixed) and conditional model (random) parts

  • Transform f to \(\eta_p^2\) (when using afex::mixed)

#get eta for model

F_to_eta2(43.75,1,  52.09)

# get r2 
r2(max_model)

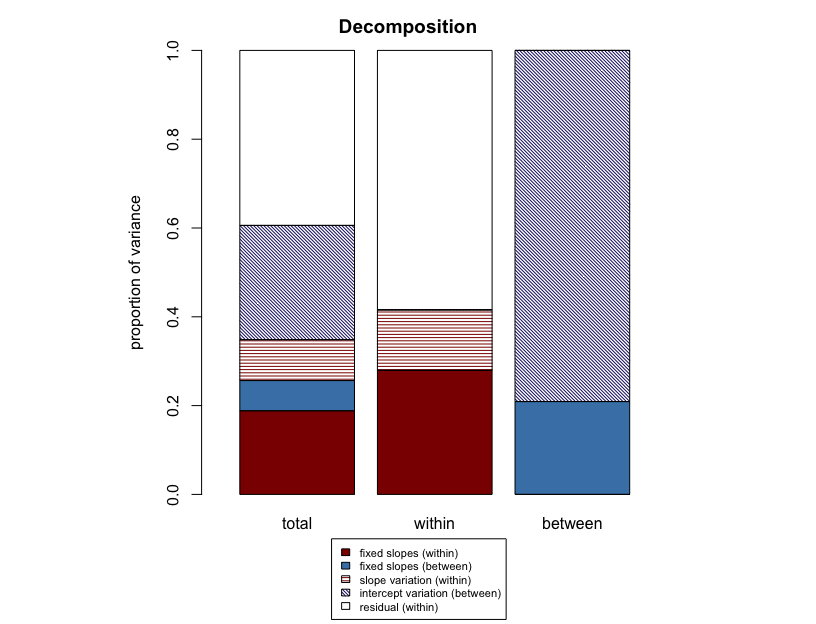
r2mlm

# install.packages("devtools")
#devtools::install_github#("mkshaw/r2mlm")

r2mlm::r2mlm(max_model)

Write-up

report::report(max_model)
We fitted a linear mixed model (estimated using REML and nloptwrap optimizer)
to predict mean_pupil with vocoded (formula: mean_pupil ~ vocoded). The model
included vocoded as random effects (formula: ~1 + vocoded | subject). The
model's total explanatory power is weak (conditional R2 = 0.08) and the part
related to the fixed effects alone (marginal R2) is of 1.34e-03. The model's
intercept, corresponding to vocoded = NS, is at 3.64e-03 (95% CI [-7.38e-04,
8.02e-03], t(5603) = 1.63, p = 0.103). Within this model:

  - The effect of vocoded [V6] is statistically significant and positive (beta =
3.12e-03, 95% CI [2.75e-04, 5.97e-03], t(5603) = 2.15, p = 0.032; Std. beta =
0.07, 95% CI [6.49e-03, 0.14])

Standardized parameters were obtained by fitting the model on a standardized
version of the dataset. 95% Confidence Intervals (CIs) and p-values were
computed using a Wald t-distribution approximation.

Table

modelsummary::modelsummary(max_model, output = "html")
 (1)
(Intercept) 0.004
(0.002)
vocodedV6 0.003
(0.001)
SD (Intercept subject) 0.012
SD (vocodedV6 subject) 0.005
Cor (Intercept~vocodedV6 subject) −0.195
SD (Observations) 0.041
Num.Obs. 5609
R2 Marg. 0.001
R2 Cond. 0.077
AIC −19801.7
BIC −19761.9
ICC 0.1
RMSE 0.04

Generalized linear mixed models

  • We can fit most of the models we talked about this semester as a multilevel model

  • Easy to fit Bayesian equivalents as well (using brms)

    # poisson
# binomial
# negative binomial

glmer(family="binomial")
glmer(family="poisson")
glmer.nb()

Shrinkage

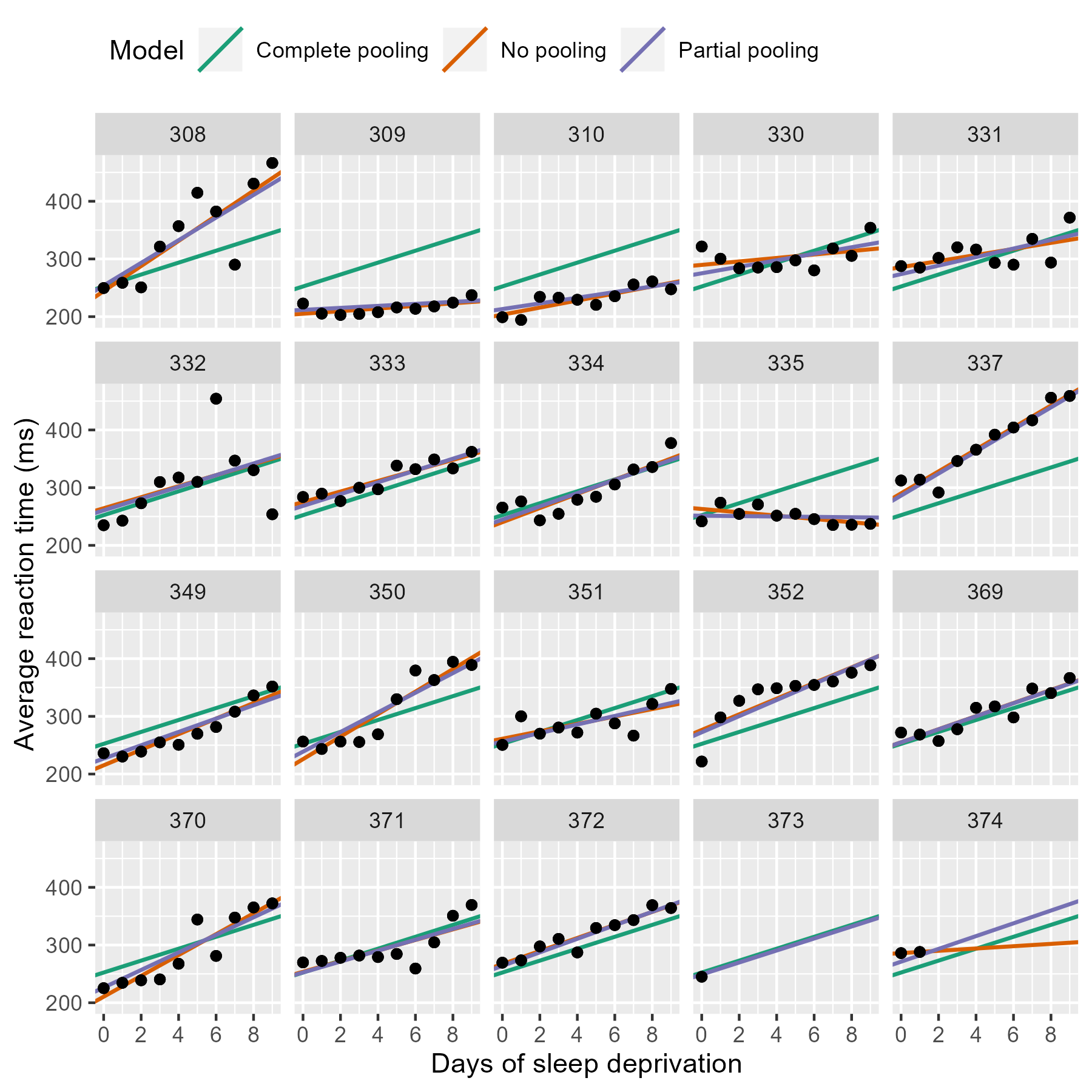
(https://www.tjmahr.com/plotting-partial-pooling-in-mixed-effects-models/)

Centering

  • You must ensure that the zero value for each predictor is meaningful before running the model

    • Categorical variables:

      • Effect-coding or contrast-coding

    • Continuous Predictors:

In MLM, there are two ways to center, by the grand mean or the group mean

Group- vs. grand-mean centering

  • Grand-mean centering: \(x_{i} - x\)

    • Variable represents each observation’s deviation from everyone’s norm, regardless of group

  • Group-mean centering: \(x_{ij} - x_j\)

    • Variable represents each observation’s deviation from their group’s norm

Group- vs. grand-mean centering

  • Level 1 predictors

    • Grand-mean center

      • Include means of level 2
      • Allows us to directly test within-group effect

    • Group-mean center

      • Level 1 coefficient will always be with within-group effect, regardless of whether the group means are included at Level 2 or not
      • If level 2 means included, coefficient represents the between-groups effect

Group mean center in R

library(datawizard) #easystats 

# how to group mean center 
d <- d %>% 
  # Grand mean centering (CMC)
  mutate(iv.gmc = iv-mean(iv)) %>%
  # Person mean centering (more generally, centering within cluster)
  group_by(id) %>% 
  mutate(iv.cm = mean(iv),
         iv.cwc = iv-iv.cm) %>%
  ungroup %>%
  # Grand mean centering of the aggregated variable
  mutate(iv.cmc = iv.cm-mean(iv.cm))
# data wizard way
x <- demean(x, select=c("x"), group="ID") #gets within-group cluster

PSY 504: Advanced Statistics