Introduction to Structural Equation Modeling in R
Princeton University
4/2/23
Structural equation modeling
A broad and extremely versatile multivariate framework
Integration of:
Path analysis (this week)
Confirmatory factor analysis (next week)
Test and quantify theories
Structural equation modeling

You already know how to do it!
It is regression on steroids
Model many relationships at once, rather than run single regressions
Model variables that exist (manifest) and those that don’t technically exist (latent factors)
Exogenous vs. endogenous variables
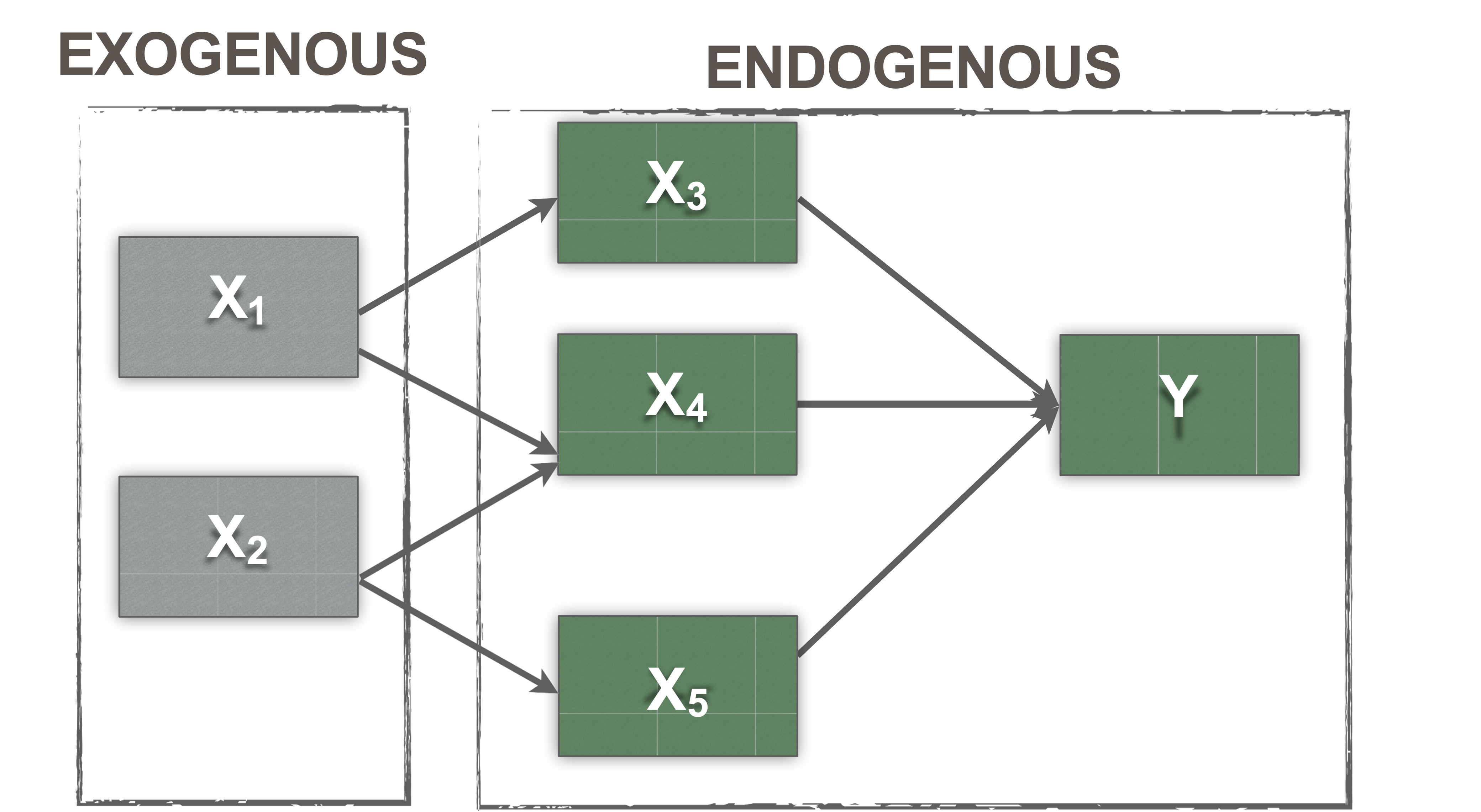
- Exogenous
- These are synonymous with independent variables
- You can find these in a model where the arrow is leaving the variable
- They are thought to be the cause of something
- Have variance
- Covary with other exogenous variables
Exogenous vs. endogenous variables

- Endogenous
- These are synonymous with dependent variables
- They are caused by the exogenous variables
- In a model diagram, the arrow will be coming into the variable
- Have error terms (disturbances)
Endogenous vs. Exogenous
TL;DR
Exogenous: no arrows pointed at it
Endogenous: arrows pointed at it
A variable can be both (example?)
Manifest variables
Manifest or observed variables
Represented by squares ❏
Measured from participants, business data, or other sources
While most measured variables are continuous, you can use categorical and ordered measures as well
Latent variables
- Latent variables
Represented by circles ◯
Abstract phenomena you are trying to model
Are not represented by a number in the dataset
Linked to the measured variables
Represented indirectly by those variables
Remember

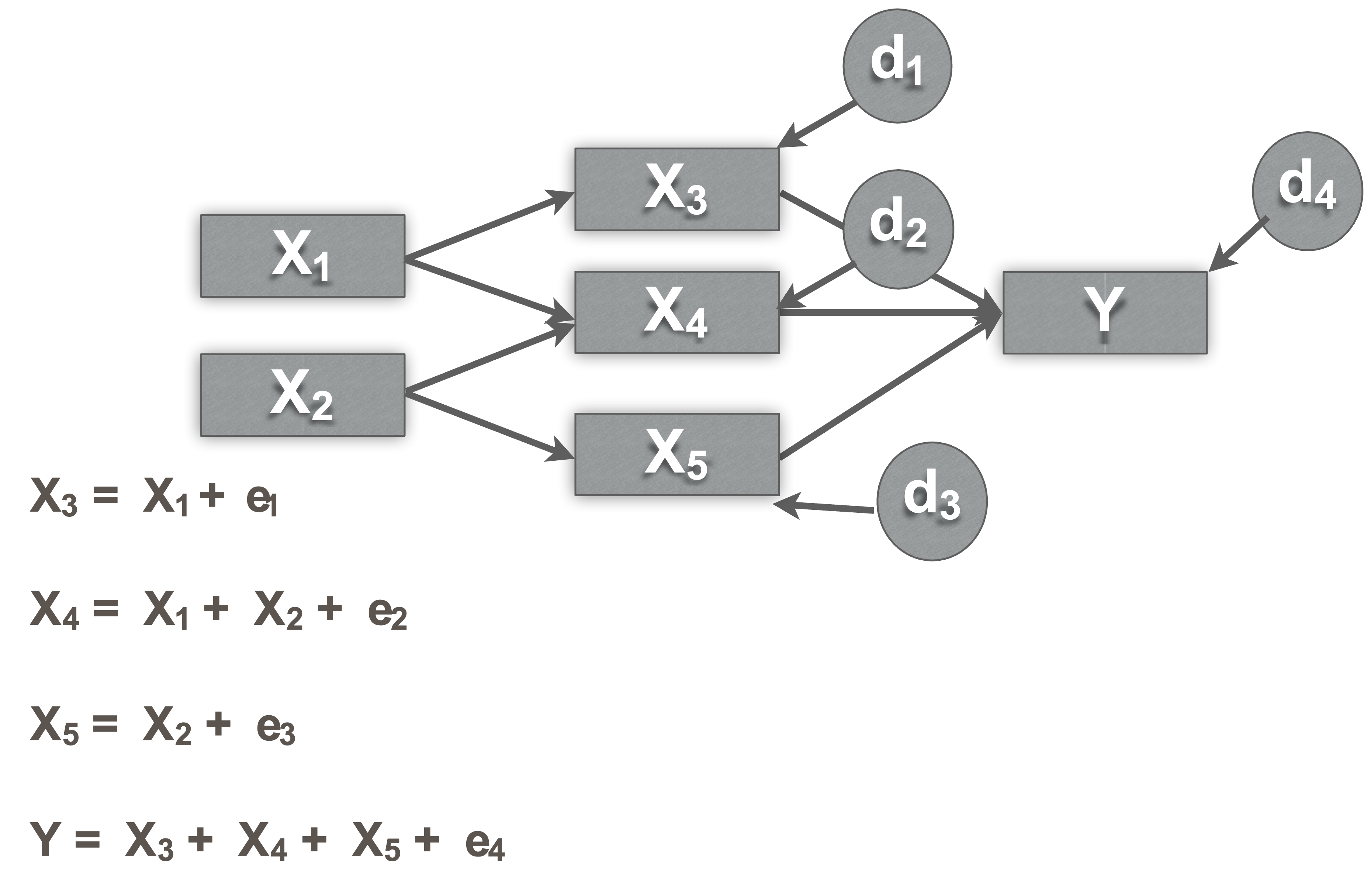
Y~X + ResidualHere that is
Endogenous ~ Exogenous + disturbance
Variances, covariances, and disturbances
Covariance paths
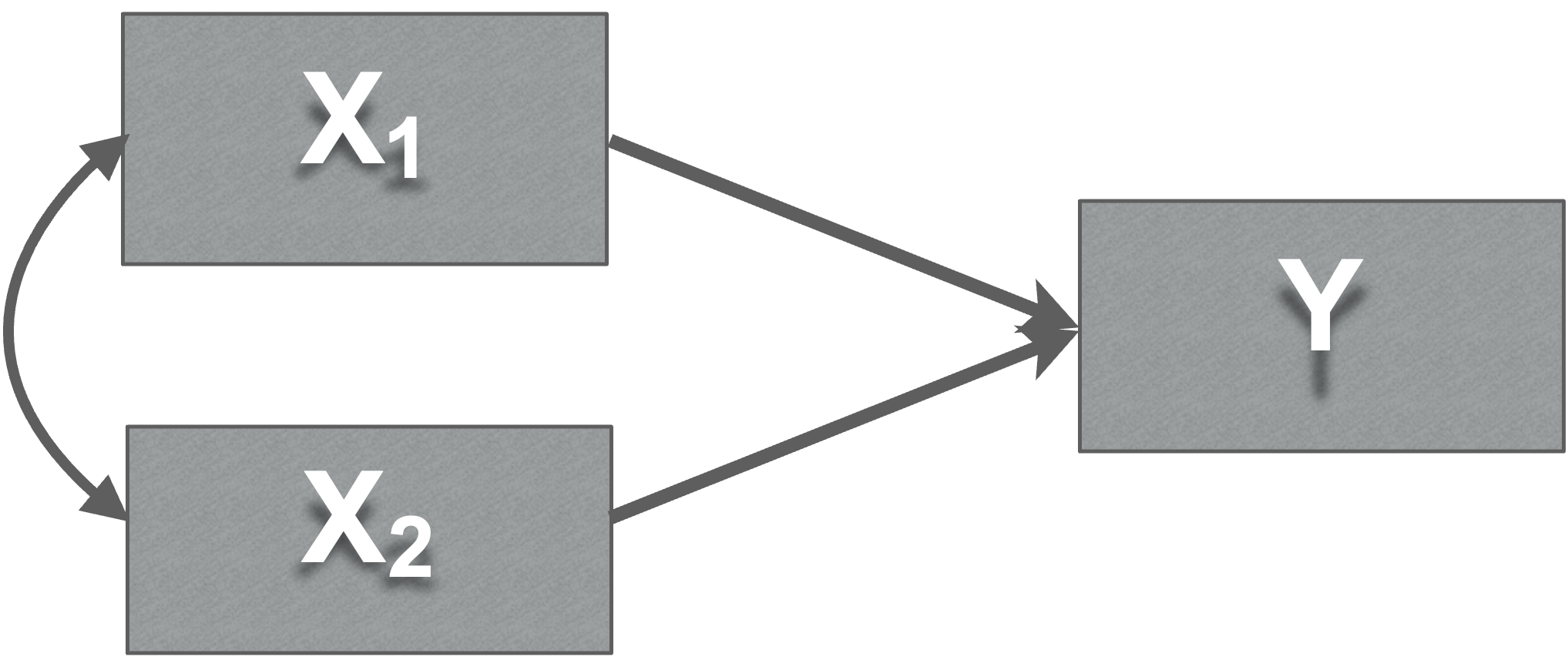
- Double headed arrows (Covariance paths)
- Exogenous variables may be correlated with each other, but not always…
Covariance meaning
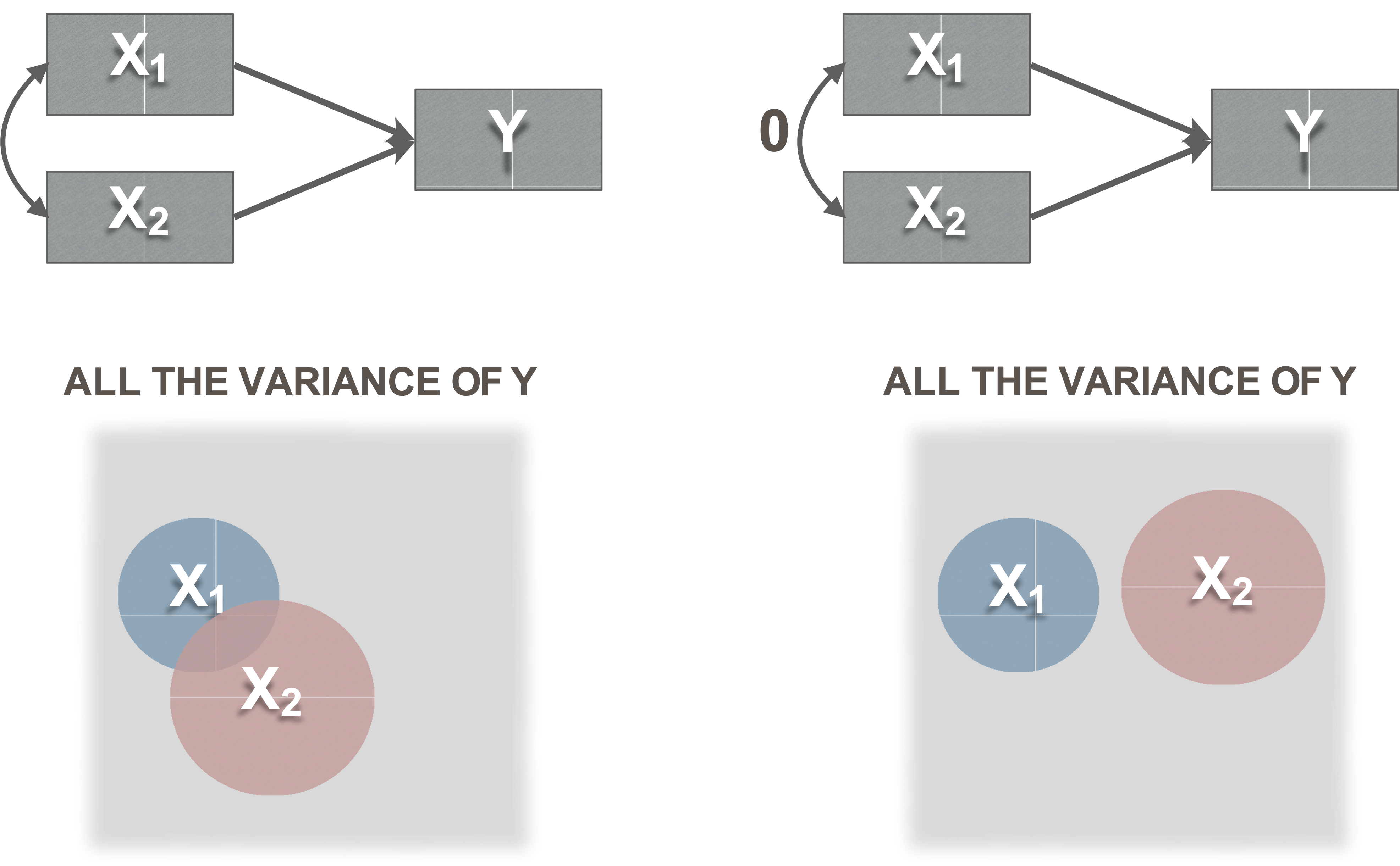
Disturbances
Represent the influence of factors not included in model
error in your prediction of each endogenous variable
Every endogenous variable has a disturbance
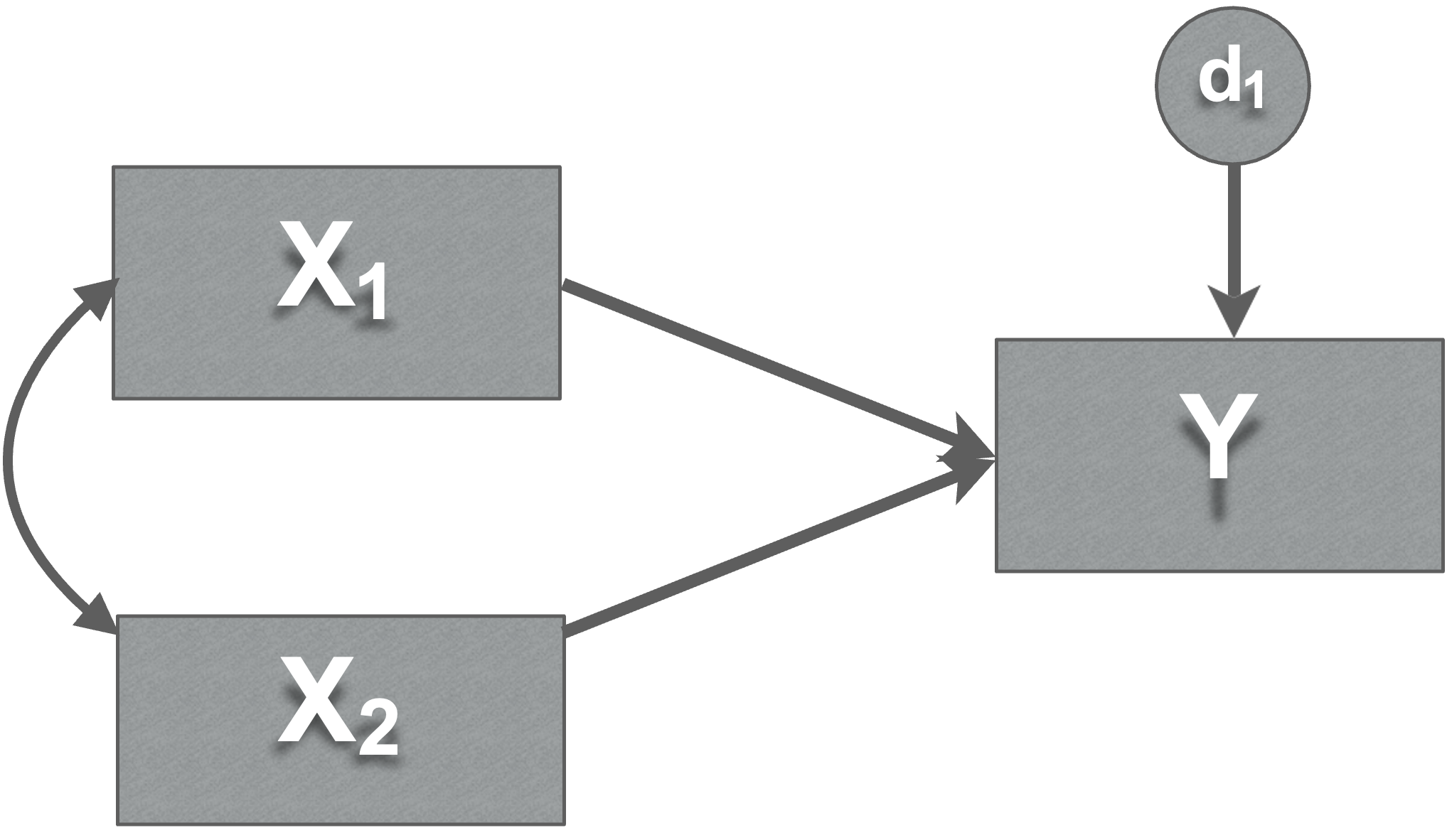
Cheat sheet
- Also here: https://davidakenny.net/cm/basics.htm
Path models
Circles are latent (unobserved) variables
Squares are manifest (observed) variables
Path models
- Straight arrows are “causal” or directional
- Non-standardized solution -> these are your b or slope values
- Standardized solution -> these are your beta values
- Curved arrows are non-directional
- Non-standardized -> covariance
- Standardized -> correlation
Why is it just regression?
Each endogenous variable is regressed on all exogenous variables that are connected in the chain that leads directly to it
![]()
Model specification
You cannot test all models
- Unique solution
If not identified, cannot analyze model
How is this determined?
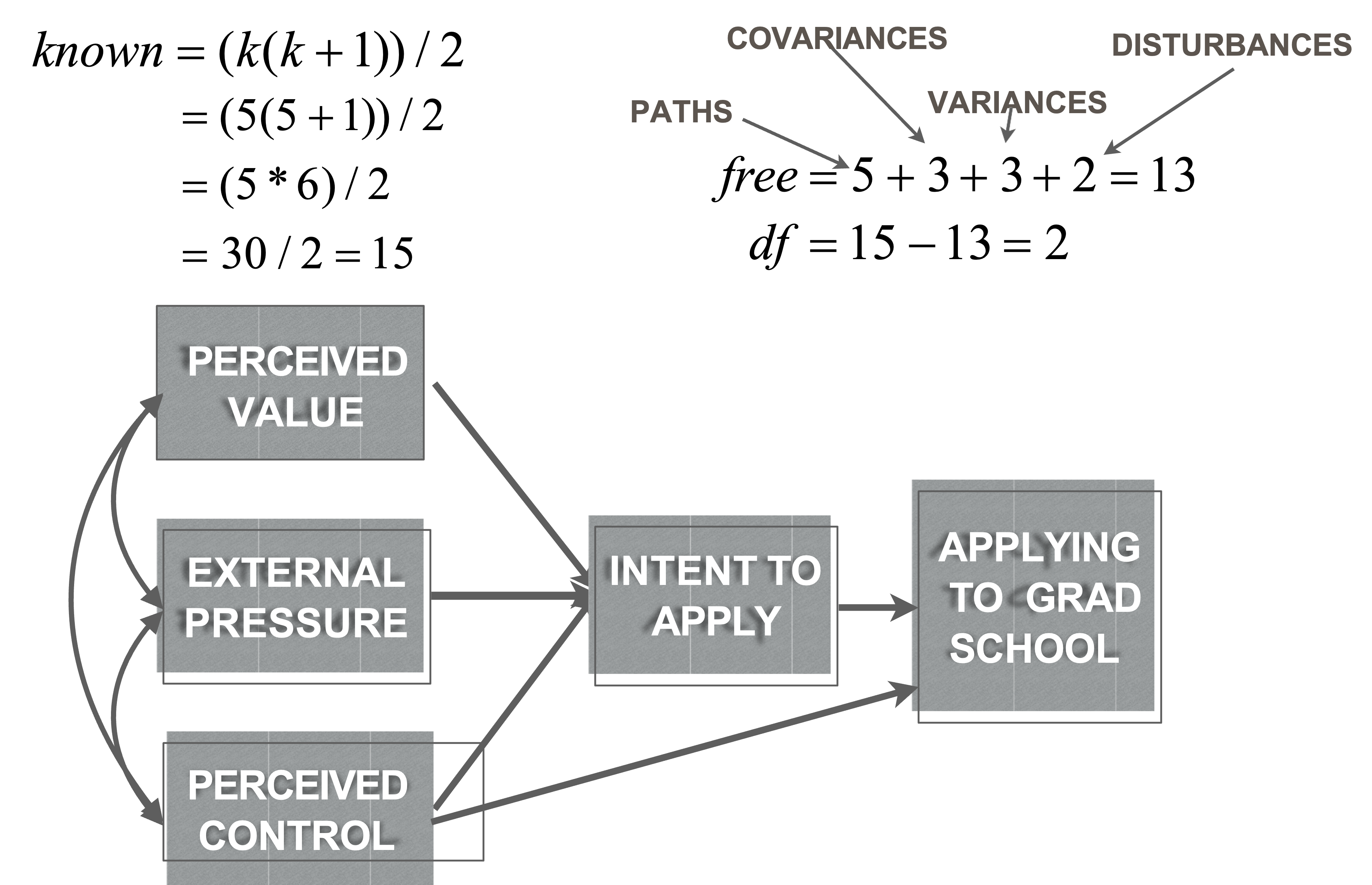
Minimum condition of identification
There must be at least as many known values in the model as there are free parameters
Free parameters:
- All regression paths, all covariances, all variances, and all disturbances in the model
Knowns:
\[\frac{(K (K+1))}{2}\] - where k is number of measured variables
Identification
Math example:
10=2x+y
2 = x-y
2 knowns and 2 unknowns
One set of values that can solve the equation
Can’t test other models
Identification
10=2x+y
2 = x-y
5 = x + 2y
![]()
- Several possible approximate solutions to solve all 3 equations. Several unique but imperfect solutions means multiple models can be tested or compared. You can’t evaluate fit without alternatives.
Model identification
We can tell model is identified by calculating model DFs
Additional pathways you can estimate
Model DF = (known values) - (free parameters)
If model DF >=1 you can analyze model
- Over-identified
Just-identified (saturated) model
DF = 0
You can still analyze the model
But:
Fits data perfectly
No fit indices
Multiple regressions are just-identified model
Estimate DFs
Let’s play a game
![]()
![]()
SEM steps
- Specify model
- Make sure it is identified
- Run the model
- Interpret output
- Report results
Model specification
- Think up all the constructs that are relevant to model
- Consider how they are connected
- Justify each path that is present and absent
- What are the hypothesized relationships?(ivs, dvs, mediators, moderators)
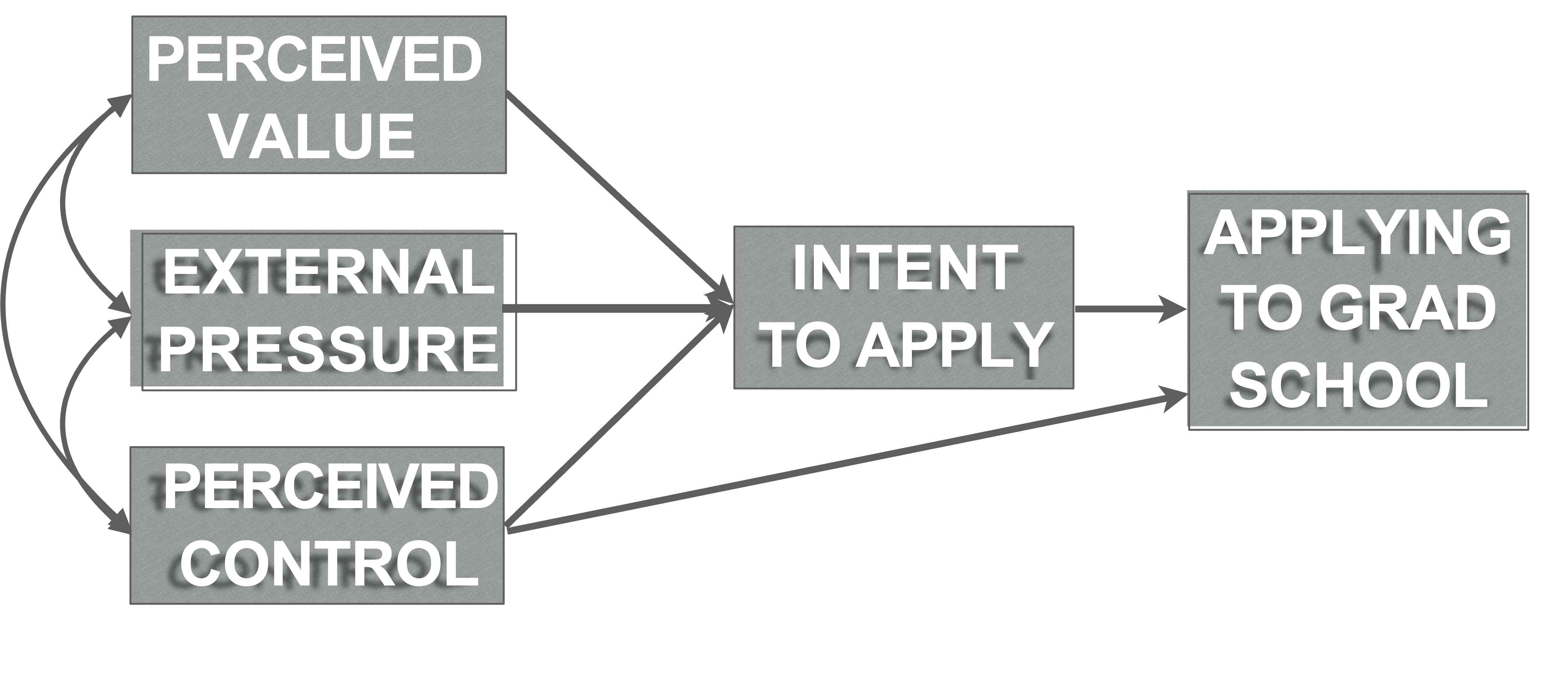
Example data (Ingram et al., 2000)
What makes someone apply to graduate school?
Endogenous
- Intent to apply (intent.to.apply)
- Apply (application.behaviour)
Exogenous:
- Perceived value (perceived.value)
- External pressure (external.pressure)
- Perceived control over admission (perceived.control)
Model`
Data screening
Identification
Run SEM in R
Declare equations for every endogenous variable in your model
Declare indirect and covariances
`~` indicates a regression
`~~` indicates a covariance/correlation
`=~` indicates a latent variable
*=name of variable
grad_model = '
intent.to.apply~a*perceived.value+b*external.pressure+c*perceived.control
application.behaviour~d*intent.to.apply+perceived.control
#indirect
value.through.intent:=a*d
#indirect
pressure.through.intent:=b*d
control.through.intent:=c*d
perceived.control ~~ perceived.value # These are covariance paths
perceived.control ~~ external.pressure # These are covariance paths
external.pressure ~~ perceived.value # These are covariance paths
'
fit <- sem(grad_model, se="bootstrap", data=grad)Model fit
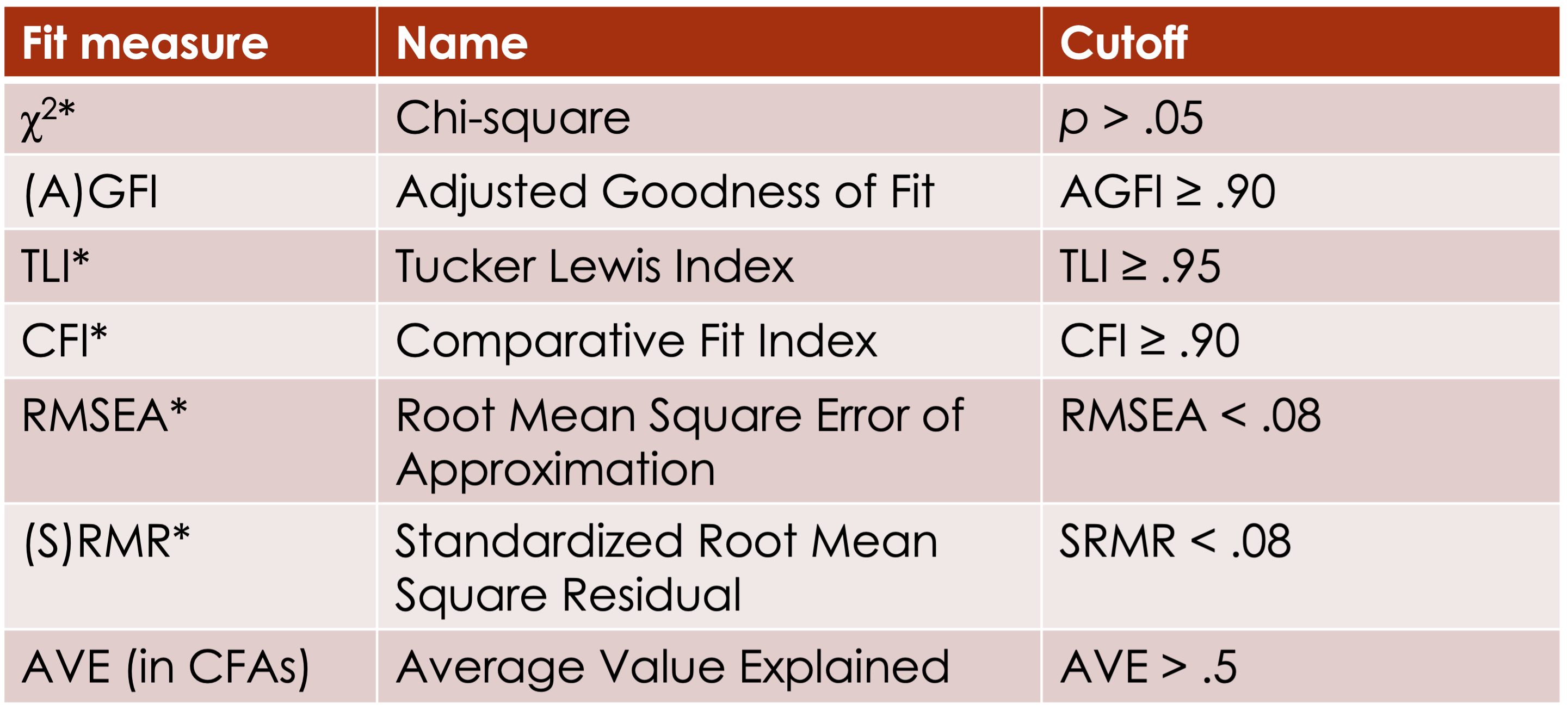
- Common to use \(\chi^2\), RMSEA, SRMR, CFI
Model fit
Absolute fit (measures how well data fits specified model)
\(\chi^2\)
SRMR
- Standardized difference between the sample covar matrix and hypothesized covar matrix
Badness of fit
RMSEA
- Measures how much worse the data fits the model from the just identified model
Relative goodness of fit
- CFI or Tucker Lewis Index
- Measures how much better the model fits than the null model (all paths=0)
- CFI or Tucker Lewis Index
Run SEM
fit <- sem(grad_model, se="bootstrap", data=grad)
summary(fit, ci=TRUE, standardize=TRUE, fit.measures=TRUE)lavaan 0.6.15 ended normally after 60 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 13
Number of observations 60
Model Test User Model:
Test statistic 0.862
Degrees of freedom 2
P-value (Chi-square) 0.650
Model Test Baseline Model:
Test statistic 136.416
Degrees of freedom 10
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 1.000
Tucker-Lewis Index (TLI) 1.045
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -993.733
Loglikelihood unrestricted model (H1) -993.303
Akaike (AIC) 2013.467
Bayesian (BIC) 2040.693
Sample-size adjusted Bayesian (SABIC) 1999.805
Root Mean Square Error of Approximation:
RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.200
P-value H_0: RMSEA <= 0.050 0.690
P-value H_0: RMSEA >= 0.080 0.257
Standardized Root Mean Square Residual:
SRMR 0.019
Parameter Estimates:
Standard errors Bootstrap
Number of requested bootstrap draws 1000
Number of successful bootstrap draws 1000
Regressions:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
intent.to.apply ~
percevd.vl (a) 0.444 0.058 7.630 0.000 0.315 0.553
extrnl.prs (b) 0.029 0.034 0.860 0.390 -0.035 0.099
prcvd.cntr (c) -0.064 0.062 -1.020 0.308 -0.199 0.056
application.behaviour ~
intnt.t.pp (d) 1.520 0.542 2.802 0.005 0.480 2.595
prcvd.cntr 0.734 0.307 2.393 0.017 0.235 1.457
Std.lv Std.all
0.444 0.807
0.029 0.095
-0.064 -0.126
1.520 0.350
0.734 0.336
Covariances:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
perceived.value ~~
perceivd.cntrl 34.696 10.798 3.213 0.001 16.524 58.825
external.pressure ~~
perceivd.cntrl 46.660 12.947 3.604 0.000 22.482 72.197
perceived.value ~~
external.prssr 39.758 11.519 3.452 0.001 18.269 63.729
Std.lv Std.all
34.696 0.665
46.660 0.505
39.758 0.472
Variances:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
.intent.to.pply 5.780 0.974 5.932 0.000 3.517 7.254
.applicatn.bhvr 179.514 28.108 6.386 0.000 115.792 224.946
perceived.valu 47.616 9.519 5.002 0.000 31.137 67.064
external.prssr 149.236 22.284 6.697 0.000 104.931 190.640
perceivd.cntrl 57.154 13.773 4.150 0.000 32.634 86.664
Std.lv Std.all
5.780 0.400
179.514 0.657
47.616 1.000
149.236 1.000
57.154 1.000
Defined Parameters:
Estimate Std.Err z-value P(>|z|) ci.lower ci.upper
val.thrgh.ntnt 0.675 0.255 2.648 0.008 0.192 1.205
prssr.thrgh.nt 0.045 0.058 0.774 0.439 -0.057 0.184
cntrl.thrgh.nt -0.097 0.120 -0.807 0.420 -0.411 0.065
Std.lv Std.all
0.675 0.282
0.045 0.033
-0.097 -0.044What to report?
Reporting Results
The model is not significantly different from a baseline model (Chi2(2) = 0.86,
p = 0.650). The GFI (.99 > .95) suggest a satisfactory fit. The PNFI (.20 <
.50) suggests a poor fit., The model is not significantly different from a
baseline model (Chi2(2) = 0.86, p = 0.650). The AGFI (.96 > .90) suggest a
satisfactory fit. The PNFI (.20 < .50) suggests a poor fit., The model is not
significantly different from a baseline model (Chi2(2) = 0.86, p = 0.650). The
NFI (.99 > .90) suggest a satisfactory fit. The PNFI (.20 < .50) suggests a
poor fit., The model is not significantly different from a baseline model
(Chi2(2) = 0.86, p = 0.650). The NNFI (.05 > .90) suggest a satisfactory fit.
The PNFI (.20 < .50) suggests a poor fit., The model is not significantly
different from a baseline model (Chi2(2) = 0.86, p = 0.650). The CFI (.00 >
.90) suggest a satisfactory fit. The PNFI (.20 < .50) suggests a poor fit., The
model is not significantly different from a baseline model (Chi2(2) = 0.86, p =
0.650). The RMSEA (.00 < .05) suggest a satisfactory fit. The PNFI (.20 < .50)
suggests a poor fit., The model is not significantly different from a baseline
model (Chi2(2) = 0.86, p = 0.650). The SRMR (.02 < .08) suggest a satisfactory
fit. The PNFI (.20 < .50) suggests a poor fit., The model is not significantly
different from a baseline model (Chi2(2) = 0.86, p = 0.650). The RFI (.97 >
.90) suggest a satisfactory fit. The PNFI (.20 < .50) suggests a poor fit. and
The model is not significantly different from a baseline model (Chi2(2) = 0.86,
p = 0.650). The IFI (.01 > .90) suggest a satisfactory fit. The PNFI (.20 <
.50) suggests a poor fit.Reporting results
- Make reference to a figure with your hypothesized model and parameter estimates and report model fit.
- The hypothesized model was tested with path analysis and the estimated model is depicted in Figure 1. The model appeared to have good fit χ2 (2) = 0.862, p > .650, SRMR = .02, RMSEA= 0, 90% CI [0, 0.20], CFI = 1.
Reporting results
- Describe significance of the paths
- The perceived value of graduate education predicted intentions to apply to grad school, β = 0.81, Z = 7.21, p < 0.01, but intentions to apply to grad school were not significantly predicted by external pressure to go to grad school, β = 0.10, Z = 0.97, p = 0.33, or perceived control over the outcome of graduate admissions, β =-0.13, Z = -1.11, p =.27. However, intention to go to grad school significantly predicted actually applying, β = 0.35, Z = 2.94, p < 0.01, and so did perceived control over the outcome of graduate admissions, β = 0.34, Z = 2.83, p = 0.01.
Visualize model
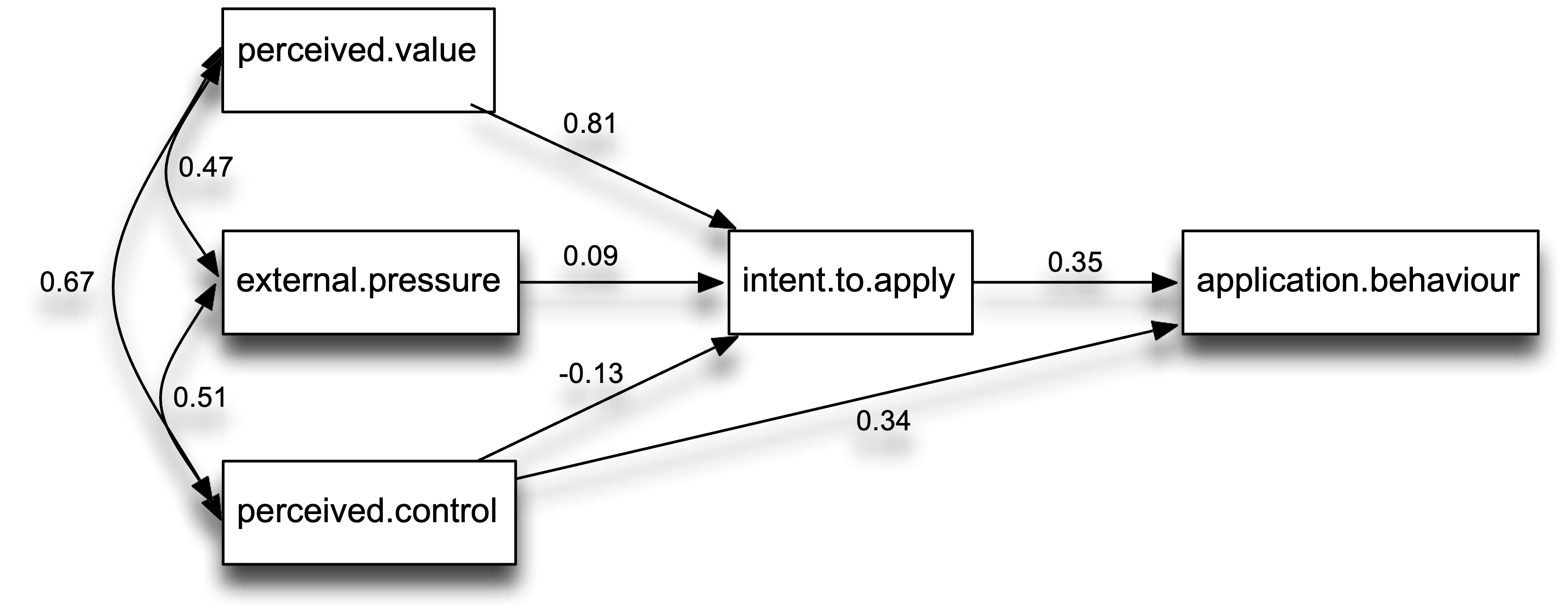
Visualize model
#| fig.align: center
#|
library(semPlot)
# Example of plotting the variables in specific locations
locations = matrix(c(0, 0, .5, 0, -.5, .5, -.5, 0, -.5, -.5), ncol=2, byrow=2)
labels = c("Intent\nTo Apply","Application\nBehaviour","Perceived\nValue","External\nPressure","Perceived\nControl")
diagram = semPaths(fit, whatLabels="std", nodeLabels = labels, layout=locations, sizeMan = 12, rotation=2)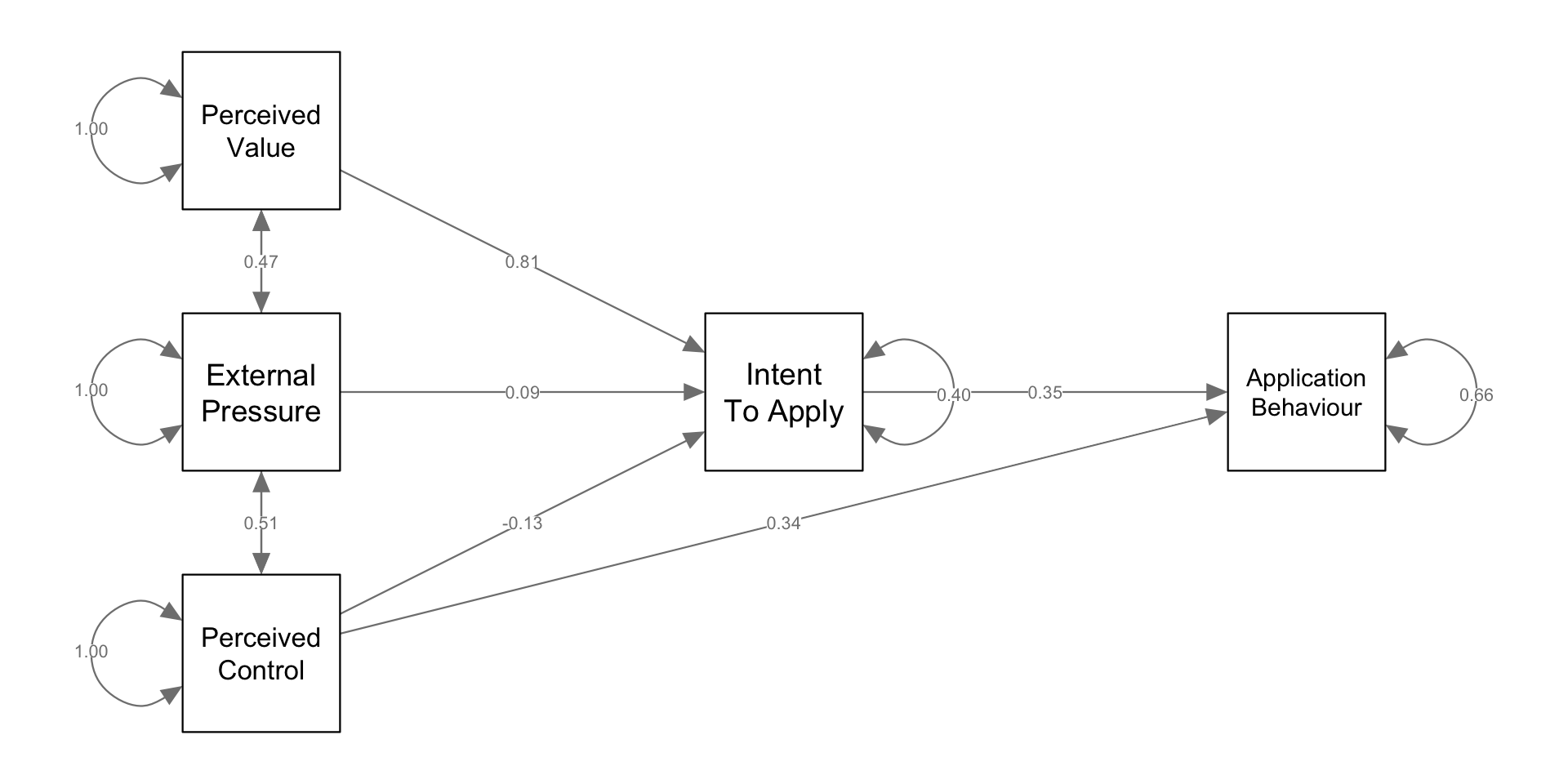
Bad fit?
Modification (mod) indices
Tell you what the chi-square change would be if you added the path suggested
Can make your model better
- Potential for HARKING!
- Be transparent
Modifications
| lhs | op | rhs | mi | epc | sepc.lv | sepc.all | sepc.nox |
|---|---|---|---|---|---|---|---|
| intent.to.apply | ~ | application.behaviour | 0.503 | -0.0234 | -0.0234 | -0.102 | -0.102 |
| application.behaviour | ~ | perceived.value | 0.35 | 0.277 | 0.277 | 0.116 | 0.116 |
| application.behaviour | ~ | external.pressure | 0.561 | 0.126 | 0.126 | 0.0934 | 0.0934 |
| perceived.value | ~ | application.behaviour | 0.137 | 0.024 | 0.024 | 0.0575 | 0.0575 |
| external.pressure | ~ | application.behaviour | 0.43 | 0.0654 | 0.0654 | 0.0885 | 0.0885 |
| perceived.control | ~ | application.behaviour | 0.787 | -0.089 | -0.089 | -0.195 | -0.195 |
Best practices
Comparing multiple models
Constraining paths
Assess alternative hypotheses/models
Sample size
Assumptions
Best practices
Constraining paths
In SEM you can explicitly test hypotheses about the size of specific paths
Constrain a path to certain value
Constrain two paths to be equal
- Compare model fit of models with constrained and unconstrained paths
Constraining paths
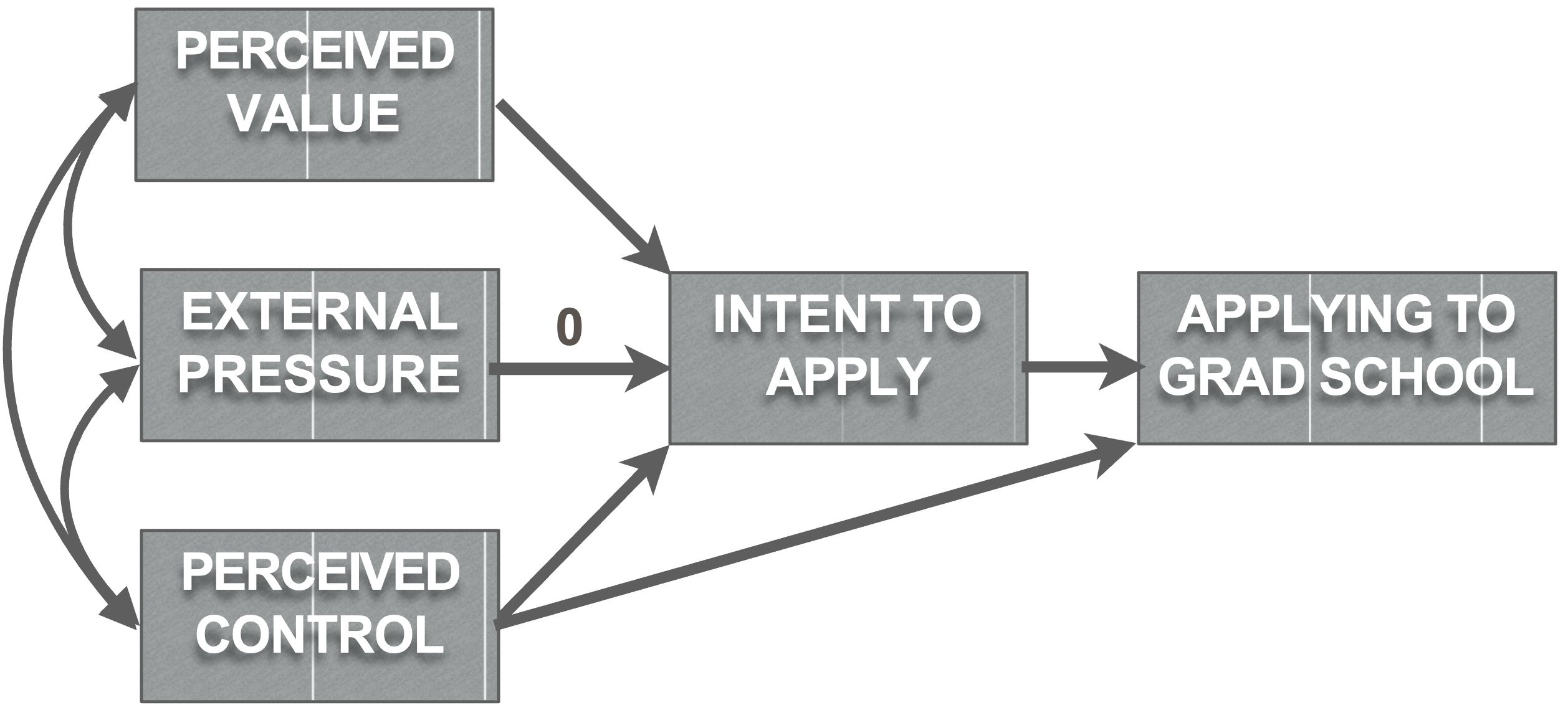
grad_model_constrained = '
intent.to.apply ~ a*perceived.value + 0*external.pressure + c*perceived.control
application.behaviour ~ d*intent.to.apply + perceived.control
perceived.control ~~ perceived.value # These are covariance paths
perceived.control ~~ external.pressure # These are covariance paths
external.pressure ~~ perceived.value # These are covariance paths
value.through.intent:=a*d
control.through.intent:=c*d
'
grad_analysis_constrained =
sem(grad_model_constrained, data=grad, se="bootstrap")LRT test
- \(\Delta\) \(\chi^2\)
Nested model comparisons
If you can create one model from another by the addition or subtraction of parameters, then it is nested
Model A is said to be nested within Model B, if Model B is a more complicated version of Model A
Evaluating models
Ensure both fit data well
- Report comparative fit indices
- If no sucks, don’t compare them
Use LRT test
- anova(model_1, model_2)
Non-nested model comparisons
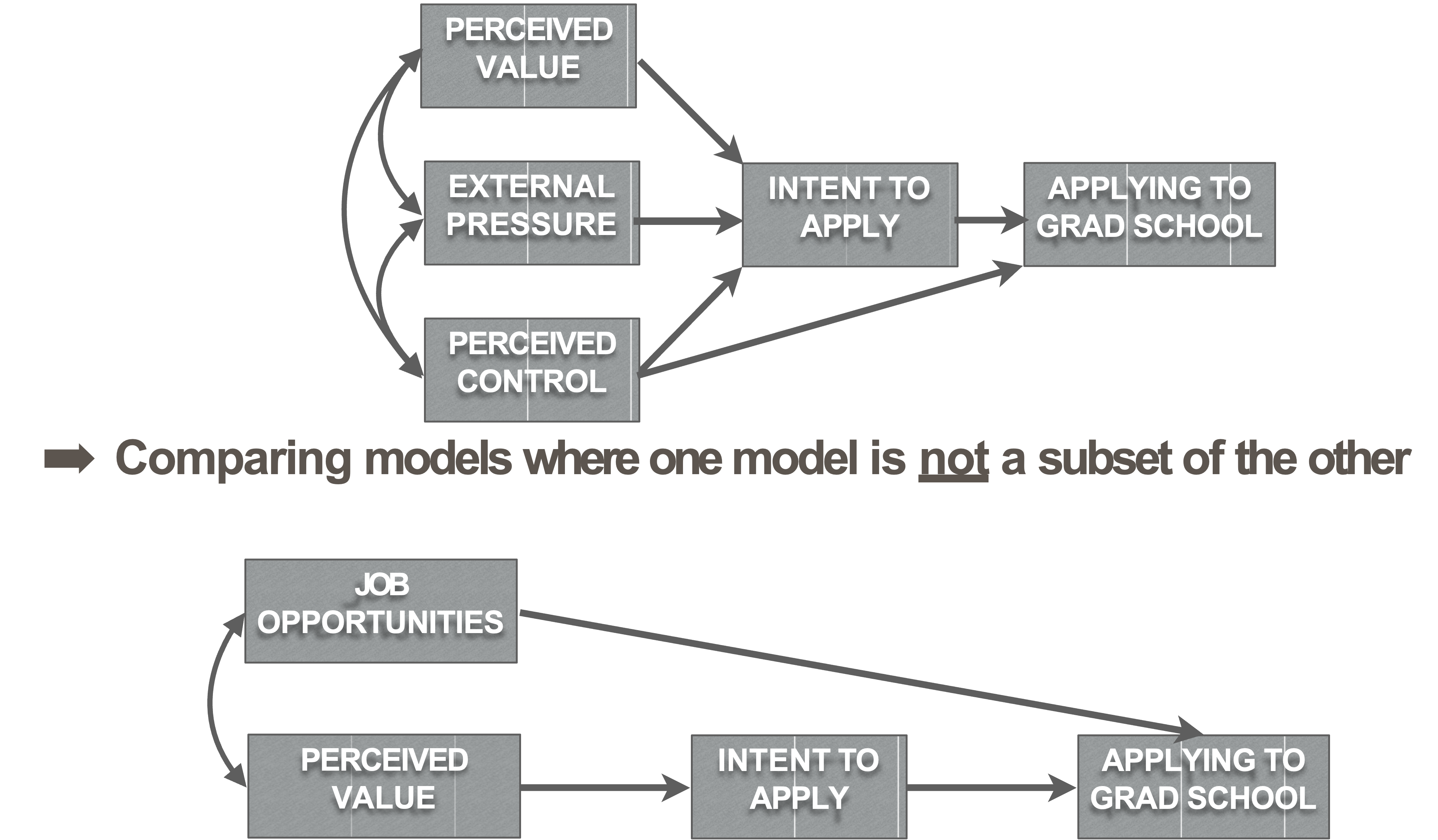
Ensure both models fit well
If so compare models with AIC or BIC
\(\Delta{BIC}\) (log odds of model with lower BIC)
- >6 strong evidence for model
If not, choose model that fits
Use
compare_performance()fromeasystats
Write-up: Nested models
We wanted to see if the data fit Ajzen’s (1985) Theory of planned behavior (“Unconstrained Model,” Figure 1) better than a constrained model that posits no relationship between external pressure and intention to apply to graduate school (“Constrained Model,” Figure 2). The constrained model fit the data well, SRMR = .03, RMSEA = 0, 90% CI [0, 0.18], CFI = 1, AIC = 2000.42, BIC = 2012.98. A Likelihood Ratio test of the two models suggested that the models fit the data equally well, \(\chi^2\) (1) = 0.95, p = 0.33. Thus, we trimmed this path in the interest of parsimony.
Write-up: Non-nested
We also compared a non-nested model that considered the strongest pathway of our originally hypothesized model in the context of job opportunities (“Opportunities Model,” Figure 3). The opportunities model had good absolute and relative goodness of fit but the relative badness of fit was poor, SRMR = .05, RMSEA =0.28, 90% CI [0.13, 0.44], CFI = 0.96, AIC = 1502.77, BIC = 1519.52. Comparing the Opportunities Model to the Hypothesized Model (Figure 1) using BIC (Kass & Raftery, 1995) reveals that the evidence strongly favors the Opportunities Model, \(BIC_{Hypothesized}\) = 2040.69, ΔBIC= 521.
Practical issues
- Sample size: for parameter estimates to be accurate, you should have large samples
- How many? Hard to say, but often hundreds are necessary
- http://web.pdx.edu/~newsomj/semclass/ho_sample%20size.pdf
- https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4334479/
Practical issues
- Sample Size: The N:q rule
- Number of people, N
- q number of estimated parameters
- You want the N:q ratio to be 20:1 or greater in a perfect world, 10:1 if you can manage it.
Assumptions
- All assumptions for linear models apply to SEM
- Normality
- There are robust estimators one can use
- Sattorra-Bentler
sem(test="satorra.bentler")
- Sattorra-Bentler
Acknowledgments
- Thanks to Elizabeth Page-Gould, Chris Groves, and Erin Buchanan for graciously providing some of the content I used here
PSY 504: Advanced Statistics